嫖了各种大佬的博客！

仿射密码 Affine Cipher

概述

仿射密码也属于单表代换密码，它使用线性方程加上一个模数。

仿射密码为单表加密的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。

算法实现

加密算法

仿射密码的加密算法是一个线性变换，是移位密码和乘数密码的组合，即对任意的明文字符 x，选取 k1，k2 两个参数，其中 k1，k2∈Z26，且要求 gcd (k1，26)=1。

加密变换：C=k1*m+k2 (mod26)（当 k1=1 时，移位密码；当 k2=1 时，乘数密码）；

加密的功能：①基本的仿射加密完全实现，大写转成大写，小写转成小写；

②判断出 k1 与 26 不互素时利用跳转语句 goto 提示 k1 输入错误，需要重新输入；

③字母外的字母保持原来的状态，不作任何处理，按照输入的样子输出；

④利用 cin.getline () 语句和 cin.ignore () 语句，确保在 while (true) 的条件下可以反复进行加密。

	int len=strlen(s);
	int m[maxn];
// 将字符移位操作的位数存到数组 m [maxn] 里面 
	for(int i=0;i<len;i++)
	{		
        if(s[i]>='A'&&s[i]<='Z')
		m[i]=(k1*(int)(s[i]-'A')+k2)%26;
		else if(s[i]>='a'&&s[i]<='z')
		m[i]=(k1*(int)(s[i]-'a')+k2)%26;
//		cout<<(char)('A'+m);
	}
	cout<<"******Encryption******"<<endl;
	cout<<"The ciphertext is:"<<endl;
	for(int i=0;i<len;i++)
	{
		if(s[i]>='A'&&s[i]<='Z')
		cout<<(char)('A'+m[i]);
		else if(s[i]>='a'&&s[i]<='z')
		cout<<(char)('a'+m[i]);
		else
		cout<<s[i];
	}
	cout<<endl;

解密算法

解密变换：m=k1^(-1)*(C-k2)(mod26)

注：为保证仿射加密函数是一个双射函数，必须要保证 (k1，26)=1。

	int len=strlen(s);
	int m[maxn];
// 将字符移位操作的位数存到数组 m [maxn] 里面 
	for(int i=0;i<len;i++)
	{		
        if(s[i]>='A'&&s[i]<='Z')
		m[i]=(k1*(int)(s[i]-'A')+k2)%26;
		else if(s[i]>='a'&&s[i]<='z')
		m[i]=(k1*(int)(s[i]-'a')+k2)%26;
//		cout<<(char)('A'+m);
	}
	cout<<"******Encryption******"<<endl;
	cout<<"The ciphertext is:"<<endl;
	for(int i=0;i<len;i++)
	{
		if(s[i]>='A'&&s[i]<='Z')
		cout<<(char)('A'+m[i]);
		else if(s[i]>='a'&&s[i]<='z')
		cout<<(char)('a'+m[i]);
		else
		cout<<s[i];
	}
	cout<<endl;

攻击方法

穷举攻击

暴力穷举破解与解密算法相差无几，主要在于用 for 循环遍历所有的 k1 和 k2，但是应当排除 k1=1，k2=0 的无意义加密。需要注意的一点是，由于采用打表法取的 k1 值，所以 k1 的取值一定与 26 互素，就不用考虑 k1 和 26 是否互素的问题。列举出所有可能的明文（一共 311 种情况），从中找出有特定标识（如 flag\ ）或构成自然语言中有意义的单词或短语的正确明文。

	for(int j=0;j<12;j++)
	for(int k=0;k<=25;k++){
	if(!(c[j]==1&&k==0)){
// 考虑到 k1=1,k2=0 的无意义加密方式 
	for(int i=0;i<len;i++)
	{
        if(s[i]>='A'&&s[i]<='Z')
		m[i]=(inverse[c[j]]*((int)(s[i]-'A')-k+26))%26;
		else if(s[i]>='a'&&s[i]<='z')
		m[i]=(inverse[c[j]]*((int)(s[i]-'a')-k+26))%26;

统计分析攻击

假定明文字母中出现频率最高的字母是e，其次是t(统计)，设仿射加密函数为e(x)=k1x+k2(mod26)；设出现频率最高的字母偏移量为a，其次是b，e(‘e’)≡a(mod26)=>e(4)≡a(mod26)=>4k1+k2≡a(mod26)；e(‘t’)≡b(mod26)=>e(19)≡b(mod26)=>19k1+k2≡b(mod26)

两式相减得 15k1≡(b-a)(mod26) 而15的逆=7；两边相乘15的模逆k1≡7(b-a)(mod26)为防止k1取负数；k1≡7(b-a)(mod26)+26

在优化的过程中，只考虑频率出现最高的字母e，则4k1+k2≡a(mod26)=>k2≡(a-4k1)(mod26)+26；

遍历表中所有的k1值，分别求出相应的k2，则可进行依次解密，解密成功率也将显著提高。

// 统计分析攻击仿射密码 
#include<bits/stdc++.h>
using namespace std;
// 考虑使用优先级队列将数量出现最多的两个字母取出来 
//priority_queue<int,vector<int>,greater<int> >q;// 升序 
priority_queue<int,vector<int>,less<int> >q;// 降序 
const int maxn=1e4;
int num[30];
char str[maxn],str2[maxn];
int  main()
{
	int c[15]={1,3,5,7,9,11,15,17,19,21,23,25};// 与 26 互素的所有元素 
	int inverse[100];
	int temp[100]={1,9,21,15,3,19,7,23,11,5,17,25};
	memset(inverse,0,sizeof(inverse)); 
	for(int i=0;i<12;i++)
	{
		inverse[c[i]]=temp[i];
	} 
	while(true)
	{
		while(!q.empty())
		{
			q.pop();
		}// 将队列清空 
		memset(num,0,sizeof(num));
		cout<<"Please enter your ciphertext:";
		cin.getline(str,maxn);// 原始密文 
		int len=strlen(str);
	    for(int i=0;i<len;i++)
	    {
// 为方便操作，将密文转换成小写字母 
		if(str[i]>='A'&&str[i]<='Z')
		{
		str2[i]=str[i]+'a'-'A';
	    }
	    else str2[i]=str[i];
	    if(str2[i]>='a'&&str2[i]<='z')
	    {
		num[int(str2[i]-'a')]++;
		}// 统计每个字母出现的次数（不考虑大小写） 
	    }
		for(int i=0;i<26;i++)
		{
			if(num[i]!=0)
			q.push(num[i]);
		}// 把字母出现次数压到队列里进行自动排序 
		int test1=0; 
        int test2=0;
		test1=q.top();// 出现最多的次数 
		q.pop(); 
		test2=q.top();// 出现次多的次数 
//		q.pop();
		int a=0;
		int b=0;
		for(int i=0;i<26;i++)
		{
			if(num[i]==test1)
			{
				a=i;
			}// 找出出现次数最多字母偏移量 
			if(num[i]==test2)
			{
				b=i;
			}// 找出出现次数次多字母偏移量 
		}
		int k1=((b-a)*7%26+26)%26;//+26 防止出现结果出现负数 
		int k2=((a-4*k1)%26+26)%26; 
		int m[maxn];// 计算每个字母偏移量放到数组 m [maxn] 中 
	    int k3=inverse[k1];// 求出 k1 模逆 
	    for(int i=0;i<len;i++)
	    {		
		m[i]=(k3*((int)(str2[i]-'a')-k2+26))%26;
//		cout<<(char)('A'+m);
	    }
	    cout<<"******Decryption******"<<endl;
	    cout<<"k1="<<k1<<","<<"k2="<<k2<<endl; 
    	cout<<"The plaintext is:"<<endl;
     	for(int i=0;i<len;i++)
    	{
		if(str[i]>='A'&&str[i]<='Z')
		cout<<(char)('A'+m[i]);
		else if(str[i]>='a'&&str[i]<='z')
		cout<<(char)('a'+m[i]);
		else
		cout<<str[i];
	    }
    	cout<<endl;
	    cin.ignore();
	}
      return 0;
}

运行结果

加密

例如：明文是 Hello CUMT~ ，k1 是 5 ，k2 是 6，得到密文 Pajjy QCOX 。

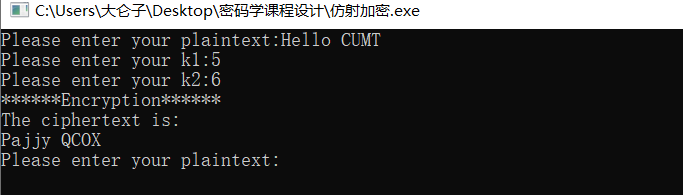
已知 key\ 解密

例如：密文是 Pajjy QCOX ，k1 是 5 ，k2 是 6，得到明文 Hello CUMT。

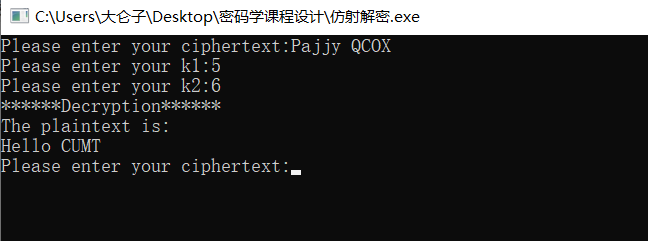
暴力枚举解密

例如：密文是 Pajjy QCOX ，不知道 k1,k2，暴力穷举出所有可能，再结合某些标识或使明文在自然语言中有意义，得到明文 Hello CUMT 。

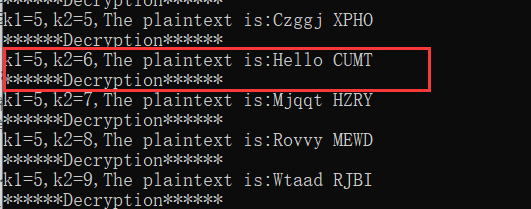
统计分析解密

例如解密：

Pu yfo of oin hvy ufa hrpkpyb, jlar ph hopkk py oin hvy oinan, svo jn jpkk klvbi rfan zfyupgnyo zlkr; pu ovayng of ufvyg iph fjy hilgfj, lmmafmaplon nhzlmn, oin hvy jpkk sn oiafvbi oin inlao,jlar nlzi mklzn snipyg oin zfayna; pu ly fvohoanozing mlkr zlyyfo ulkk svoonaukx, oiny zknyzing jlcpyb larh, bpcny mfjna; pu P zly’o ilcn sapbio hrpkn, po jpkk ulzn of oin hvyhipyn, lyg hvyhipyn hrpkn ofbnoina, py uvkk skffr.\

结果是：

If not to the sun for smiling, warm is still in the sun there, but we will laugh more confident calm; if turned to found his own shadow, appropriate escape, the sun will be through the heart,warm each place behind the corner; if an outstretched palm cannot fall butterfly, then clenched waving arms, given power; if I can’t have bright smile, it will face to the sunshine, and sunshine smile together, in full bloom.\

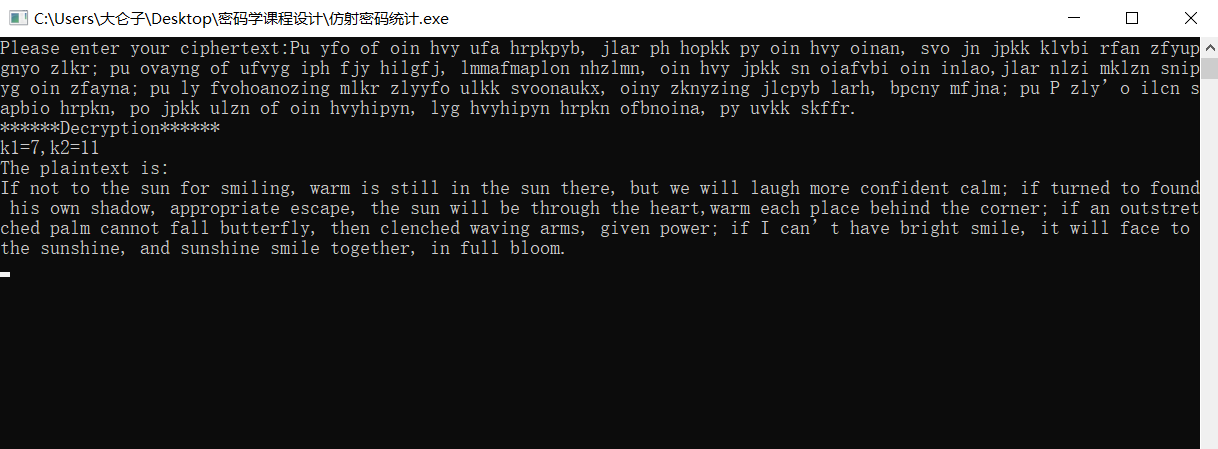
安全性分析

由于gcd(k1.26)=1，所以k1 有 φ(26)=12种取值；k2则有 26 种取值，刨除 k1=1,k2=0的情况，密钥空间为 12×26−1=311 。对于普通的偏移密码和乘法密码，仿射密码的安全性有很大的改善，但其实依然不够大，即使是使用穷举攻击，也能轻易破解出明文。但是更好的方式是根据统计分析规律（前提是截获的密文足够长）进行攻击。实际上，由于只有两个参数，所以找到两组明文密文对便可计算出两个参数，从而彻底攻破算法。

维吉尼亚密码 Vigenère cipher

概述

维吉尼亚密码是一种简单的多表代换密码，可以看成由一些偏移量不同的恺撒密码组成。为了掩盖字母使用中暴露的频率特征，解决的办法就是用多套符号代替原来的文字。它是一个表格，第一行代表原文的字母，下面每一横行代表原文分别由哪些字母代替，每一竖列代表我们要用第几套字符来替换原文。一共26个字母，一共26套代替法，所以这个表是一个26*26的表 .

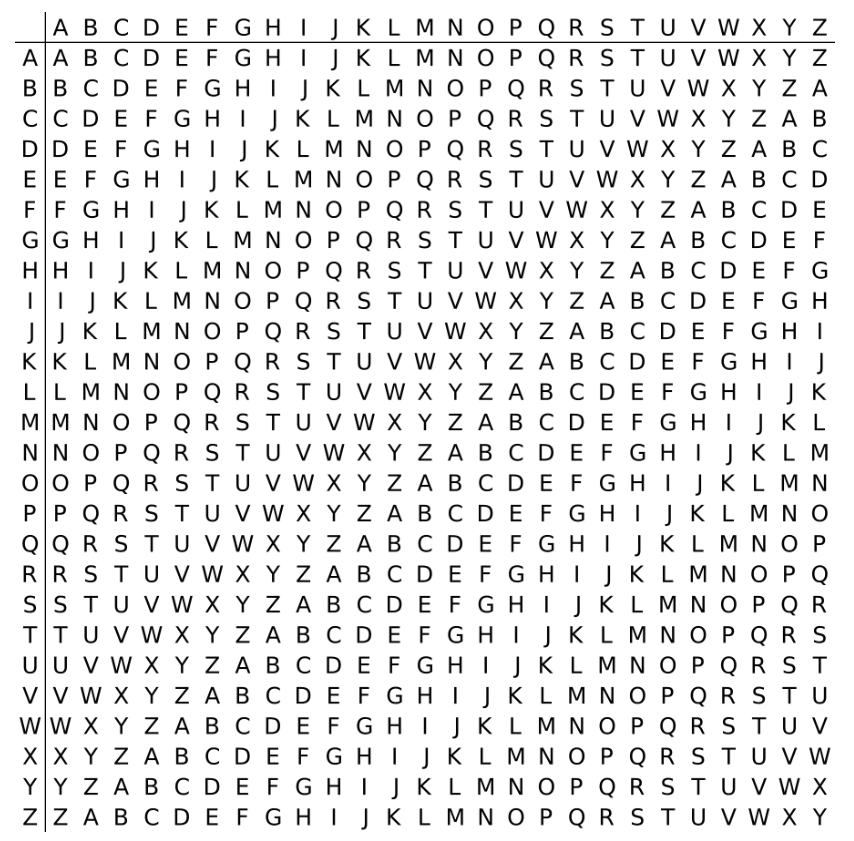
算法实现

加密算法

s2[i]=’A’+(s2[i]+(s1[j%len1]-‘a’)-‘A’)%26；

特别要注意的是，若密钥长度小于明文长度，则密钥循环使用，这体现在我们的代码中就是对 len(1) 取模。

	int j=0;
	for(int i=0;i<len2;i++)
	{
// 如果遇到空格，就不能用密钥 
// 通过 j 来进行标记 
		if(s2[i]>='A'&&s2[i]<='Z')
		{
			s2[i]='A'+(s2[i]+(s1[j%len1]-'a')-'A')%26;	
			j++;
		}
		else if(s2[i]>='a'&&s2[i]<='z')
		{
			s2[i]='a'+(s2[i]+(s1[j%len1]-'a')-'a')%26;		
			j++;
		}
		cout<<s2[i];
	}

解密算法

s2[i]=’A’+(s2[i]-‘A’-(s1[j%len1]-‘a’)+26)%26;

这里加26防止出现负数。

	int j=0;
	for(int i=0;i<len2;i++)
	{
// 如果遇到空格，就不能用密钥 
		if(s2[i]>='A'&&s2[i]<='Z')
		{
			s2[i]='A'+(s2[i]-'A'-(s1[j%len1]-'a')+26)%26;
			j++;
		}
		else if(s2[i]>='a'&&s2[i]<='z')
		{
			s2[i]='a'+(s2[i]-'a'-(s1[j%len1]-'a')+26)%26;
			j++;
		}
		cout<<s2[i];
	}

其他考虑

对于大小写字母的区分，我们的处理方法和恺撒密码中完全相同。

对于字母之外的字符，他们不使用密钥，也不消耗密钥，这时候，密文就是明文，明文就是密文。

攻击方法

破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度，那密文就可以被看作是交织在一起的凯撒密码，而其中每一个都可以单独破解。

多表代换密码体制的分析方法主要分为三步：第一步确定秘钥长度，常用的方法有卡西斯基（Kasiski）测试法和重合指数法（Index of Coincidence）；第二步就是确定秘钥，常用的方法是拟重合指数测试法；第三步是根据第二步确定的密钥恢复出明文。

Kasiski测试法

卡西斯基试验是基于类似 the 这样的常用单词有可能被同样的密钥字母进行加密，从而在密文中重复出现。如果将密文中所有相同的字母组都找出来，并计算他们的最大公因数，就有可能提取出来密钥长度信息。

测试过程：搜索长度至少为2的相邻的一对对相同的密文段，记下它们之间的距离。而密钥长度d可能就是这些距离的最大公因子

重合指数法

利用随机文本和英文文本的统计概率差别来分析密钥长度。依据：英文中每种单词出现的频率不同。

重合指数公式：

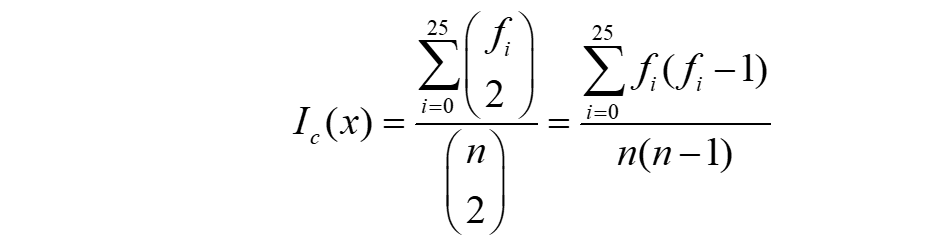
人们已经获得了英文的26个字母的概率分布的一个估计。期望值为：

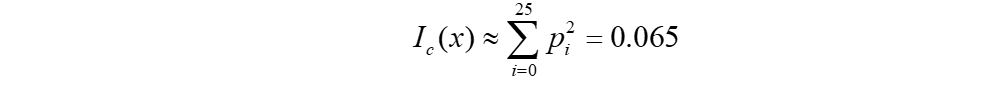
将密文按n来分组，当每组的重合指数都接近0.065时，n便为密钥的长度值

完整代码

  while(true)
 	{
    float IC[clen];// 重合指数
    memset(IC,0,sizeof(IC));
	float avgIC=0;// 平均重合指数
	for(int i=0;i<klen;i++)// 统计分组字母个数 	
	{	
	    memset(num,0,sizeof(num));// 盛放字母个数的数组
	    // 密钥长度等于分成的组数
		for(int j=0;i+j*klen<clen;j++) //统计每一组每个字母出现的次数 
		{
		if(c[i+j*klen]>='A'&&c[i+j*klen]<='Z')
		{ 
		num[(int)(c[i+j*klen]-'A')]++;
		} 
		if(c[i+j*klen]>='a'&&c[i+j*klen]<='z')
		{ 
		num[(int)(c[i+j*klen]-'a')]++;
		}
		} 
        float e=0;// 重合指数的值  重合指数是小数不能用int 
        int L=0; 
        for(int k=0;k<26;k++)// 子串密文长度 
        {
        L+=num[k];  //所有的字母数量相加 
        } //L是密文长度 
        L*=(L-1);// 分母 ,L=L*(L-1)
	    for(int k=0;k<26;k++)// 分组计算重合指数 IC 
	    {
	    if(num[k]!=0)
	    {
		e+=((float)num[k]*(float)(num[k]-1))/(float)L; //xi(xi-1)/L(L-1) 
		}
		}
		IC[i]=e;//得到无偏估计值 
	} 
	for(int i=0;i<klen;i++)
	{
	avgIC+=IC[i];
	}
	avgIC/=klen;// 求 IC 的平均值 第一次klen为1   
    if(avgIC>=0.065)break;// 判断退出条件，重合指数的平均值是否大于 0.065 
   	else klen++;
//   	cout<<"密钥长度为:"<<klen<<endl;
    }
cout<<"密钥长度为:"<<klen<<endl;
//计算拟重合指数 
	for(int i=0;i<klen;i++) // 统计分组字母个数 
	{	
	int g=0;// 密文移动 g 个位置 
	float temp[26];// 存储偏移量 
	memset(temp,0,sizeof(temp));
	for(g=0;g<26;g++)
	{
		float x=0;// 拟重合指数 	
		memset(num,0,sizeof(num));// 盛放字母个数的数组
		for(int j=0;i+j*klen<clen;j++)
		{
			if(c[i+j*klen]>='A'&&c[i+j*klen]<='Z')
			{ 
			num[(int)(c[i+j*klen]-'A')]++;
			}
			if(c[i+j*klen]>='a'&&c[i+j*klen]<='z')
			{ 
			num[(int)(c[i+j*klen]-'a')]++;
			}
		}
	    int L=0;
	    for(int k=0;k<26;k++)// 子串密文长度
		{
			L+=num[k];
			x=x+p[k]*num[(k+g)%26];
	    }
	    temp[g]=abs(x/L-0.065);
	}
	float value=temp[0]; 
	int result=0;
	for(g=0;g<26;g++)// 找最小偏差 
	{
		if(temp[g]<value)
		{
		value=temp[g];
		result=g;
		}
	}
		key[i]=result;		
	}
	cout<<"加密密钥为:";
	for(int i=0;i<klen;i++)
	{
		s2[i]=char('a'+key[i]);
	}
}

运行结果

加密

例如明文是 Haha CUMTer~ ，密钥是 password，得到密文 Wazs YIDWtr~ 。

解密

例如密文是 Wazs YIDWtr~ ，密钥是 password，得到明文 Haha CUMTer~。

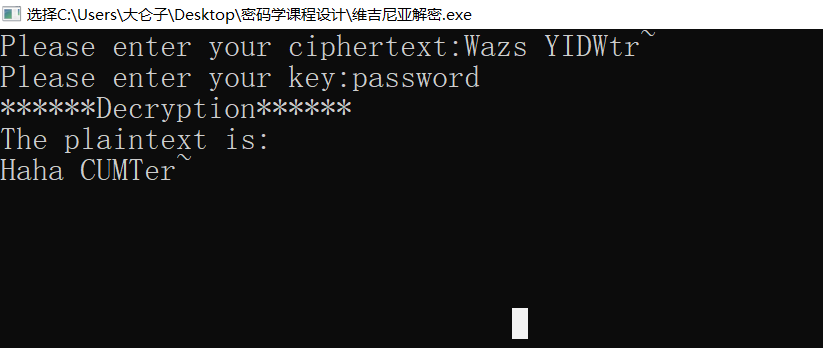
破解

例如解密：

BZGTNPMMCGZFPUWJCUIGRWXPFNLHZCKOAPGLKYJNRAQFIUYRAVGNPANUMDQOAHMWTGJDXGOMPJPTKAAVZIUIWKVTUCWBWNFWDFUMPJWPMQGPTNWXTSDPLPMWJAXUHHXWPFXXGVAPFNTXVFKOYIRBOQJHCBVWVFYCGQFGUSUBDWVIYATJGTBNDKGHCTMTWIUEFJITVUGJHHIMUVJICUWYQWYGGUWPUUCWIFGWUANILKPHDKOSPJTTWJQOJHXLBJAPZHVQWPDYPGLLGDBCHTGIZCCMEGVIIJLIFFBHSMEGUJHRXBOQUBDNASPEUCWNGWSNWXTSDPLPMWJAIUHUMWPSYCTUWFBMIAMKVBNTDMQNBVDKILQSSDYVWVXIGDQFIBHSLEAVDBXGOLGDBCHTGIZVNFQFKTNGRWXUDCTGKWCOXIXKZPPFDZG\

结果是：

THESTATEKEYLABORATORYOFNETWORKINGANDSWITCHINGTECHNOLOGYBELONGSTOBEIJINGUNIVERSITYOFPOSTSANDTELECOMMUNICATIONSTHELABORATORYWASOPENEDINNINETEENNINETYTWOINNINETEENNINETYFIVETHELABORATORYPASSEDACCEPTANCEINSPECTIONBOGOVERNMENTANDANEVALUATIONORGANIZEDBYMINISTRYOFSCIENCEANDTECHNOLOGYINTWOTHOUSANDANDTWOSINCETWOTHOUSANDANDFOURTHELABORATORYHASBEENRENAMEDASTHESTATEKEYLABORATORYOFNETWORKINGANDSWITCHINGTECHNOLOGYBYMINISTRYOFSCIENCEANDTECHNOLOGY\

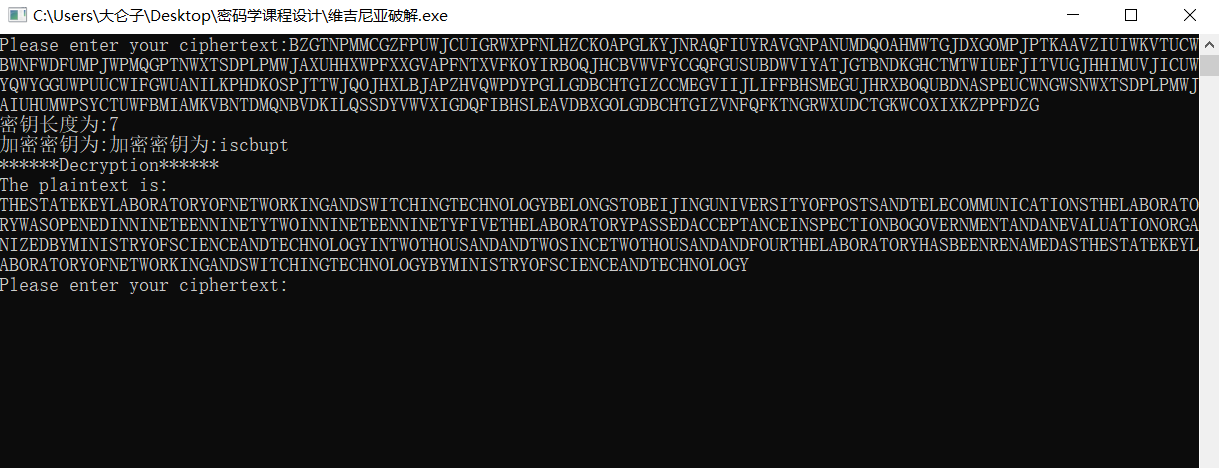
安全性分析

多表代换密码打破了原语言的字符出现规律，故其分析方法比单表代换密码复杂得多。多表代换密码对比单表代换密码安全性显著提高。但是仍然可以用一些统计分析法破解（具体参看上文攻击方法), 对所有多表密码的破译都是以字母频率为基础的，这里对维吉尼亚的分析仍不例外，只是直接的频率分析并不适用。通过卡西斯基试验或者就可以得到密钥长度，得到密钥长度，密钥就可以看作是多个凯撒密码结合到一起，每一个都可单独破解，就像上面的破解步骤。但是前提是密文足够长。所以，较短的密文几乎是不可破译的。较长的密文是很容易破解的。

序列密码 LFSR

概述

反馈移位寄存器由移位寄存器和反馈函数组成。移位寄存器是由位组成的序列，每次移位寄存器中所有位右移一位，新的最左端的位根据寄存器中的某些位计算来得到，反馈函数用来计算新的最左端位。而线性移位寄存器就是采用线性函数来作为反馈函数的反馈移位寄存器。

算法实现

开始设置好寄存器初始序列全局变量，抽头序列，再初始化一个跟寄存器长度一样的新列表。

利用zfill函数来初始化寄存器状态，定义 output_ = [] 来存放输出序列，编写feedback函数计算抽头异或的值,reg.txt记录周期内寄存器的状态。

# 20次本原多项式:x^20 + x^3 + 1
def feedbck(reg, fb):
    """
    反馈函数
    :param reg: 移位寄存器的内容
    :param fb: 由抽头构成的列表
    :return: 最左端的输入
    """
    res = reg[fb[0] - 1]
    for i in range(1, len(fb)):
        res = int(res) ^ int(reg[fb[i] - 1])
    return res
def lfsr(p):
    """
    线性反馈移位寄存器
    :param p: 由本原多项式次数构成的列表
    :return:
    """
    reg_len = max(p)
    # 初始寄存器状态:00000....001
    shift_reg = '1'.zfill(reg_len)   #在1前面补0
    regs = [shift_reg]  # 存放寄存器的各个状态
    output_ = []  # 存放输出序列
    for i in range(pow(2, reg_len) - 1):
        # 输出寄存器最右端的值
        output_.append(shift_reg[-1])
        # 计算抽头异或的值
        input_ = str(feedback(shift_reg, p))
        shift_reg = input_ + shift_reg[:-1]
        # 如果寄存器当前状态已经出现过了,说明一个周期结束
        if shift_reg in regs:
            break
        else:
            regs.append(shift_reg)
    return output_, regs
def main():
    while True:
        try:
            ct = input("\n请输入本原多项式x的系数(以空格分隔):\n").split(" ")
            if ('q' in ct) or ('Q' in ct):
                break
            ct = [int(ct[i]) for i in range(len(ct))]
            print("您输入的本原多项式为:")
            for i in range(len(ct)):
                print("x^" + str(ct[i]) + " + ", end="")
            print("1")
            print("理论最大周期为: " + str(pow(2, max(ct)) - 1))
            mode = input("是否确认:\n[Y]确定\t[N]重新输入\t[Q]退出\n")
            if mode == 'Y' or mode == 'y':
                outputs, regs = lfsr(ct)
                print("\n周期为: " + str(len(outputs)))
                choice1 = input("是否查看输出序列:\n[Y]是\t[N]否\n")
                if choice1 == 'Y' or choice1 == 'y':
                    for i in outputs:
                        print(i, end="")
                choice2 = input("\n是否输出周期内寄存器各状态:\n[Y]是\t[N]否\n")
                if choice2 == 'Y' or choice2 == 'y':
                    with open('regs.txt', 'w') as f:
                        for i in regs:
                            f.write(i + "\n")
                    print("成功！周期内寄存器各状态保存在regs.txt")
            elif mode == 'N' or mode == 'n':
                continue
            else:
                if mode == 'Q' or mode == 'q':
                    break
                else:
                    continue
        except:
            print("输入有误!")
            continue
if __name__ == '__main__':
    main()

运行结果

20次本原多项式:x^18 + x^3 + 1

寄存器初始值：[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]

本原多项式：[1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0]

安全性分析

由算法的实现可知，序列密码算法的加解密对种子秘钥的依赖十分强烈。故需要保证种子秘钥的安全性。对于此可进行相关攻击。可以进行穷举搜素攻击，故为了保证安全强度，要求秘钥长度足够长。弱密钥攻击，弱密钥会产生重复的密钥流，一旦子密钥序列出现了重复，密文就有可能被破解。序列密码具有实现简单、便于硬件实施、加解密处理速度快、没有或只有有限的错误传播等特点，因此在实际应用中，特别是专用或机密机构中保持着优势，序列密码是一个随时间变化的加密变换，具有转换速度快、低错误传播的优点，硬件实现电路更简单。

分组密码

概述

DES是分组加密，将明文分成64位一组，密钥长度 64 比特（其中有效长度为 56 比特），8 的倍数位为奇校验位（保证每 8 位有奇数个 1）。如图，64 比特的密钥经过置换选择和循环移位操作可生成 16 个 48 比特的子密钥。明文 m 经过初始置换 IP 后划分为左右两部分（各32 比特），经过 16 轮 Feistel 结果（其中最后一轮不做左右交换）再做一次逆置换 IP-1得到密文 c 。

加密方程：

解密方程：

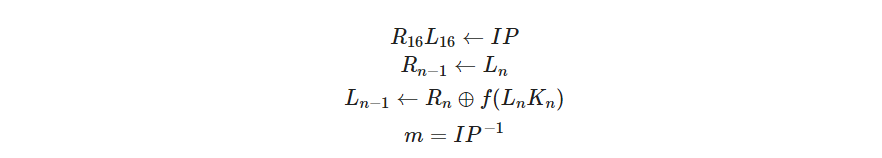
由此可见DES是一个对合运算。

密钥扩展

用于生成迭代的子密钥。具体过程为：

64位初始密钥经过置换选择1 ( PC-1 ) 后变成 56 位，经过循环左移和置换选择2 ( PC-2 ) 后分别得到 16 个 48 位子密钥 Ki 用做每一轮的迭代运算。

PC-1 去掉了校验位， PC-2 去掉了9, 18, 22, 25, 35, 38, 43, 54 位。

置换选择

置换选择1（PC-1）和置换选择2（PC-2）：

#秘钥的PC-1置换
def change_key1(my_key):
    res = ""
    for i in PC_1:
        res += my_key[i-1]
    return res

#秘钥的PC-2置换
def change_key2(my_key):
    res  = ""
    for i in PC_2:
        res += my_key[i-1]
    return res

循环左移

输入序列经过指定循环左移次数后得到结果（可以使用切片法）：

#循环左移操作
def left_turn(my_str,num):
    left_res = my_str[num:len(my_str)]
    left_res = my_str[0:num]+left_res
    return left_res

加入取模操作的好处：若 num 为负数，则相当于可以处理循环右移，方便解密时使用。

初始置换 IP 和它的逆置换 IP-1

IPIP 在第一轮迭代之前进行，目的是将原明文块的位进行换位操作（查表），实际并没有密码意义，因此在软件中时常直接被去掉。

IP−1IP−1 在最后一轮迭代之后进行，在加密算法中输出为密文，在解密算法中输出明文，若 IPIP 被去掉，IP−1IP−1 也相应地被去掉。

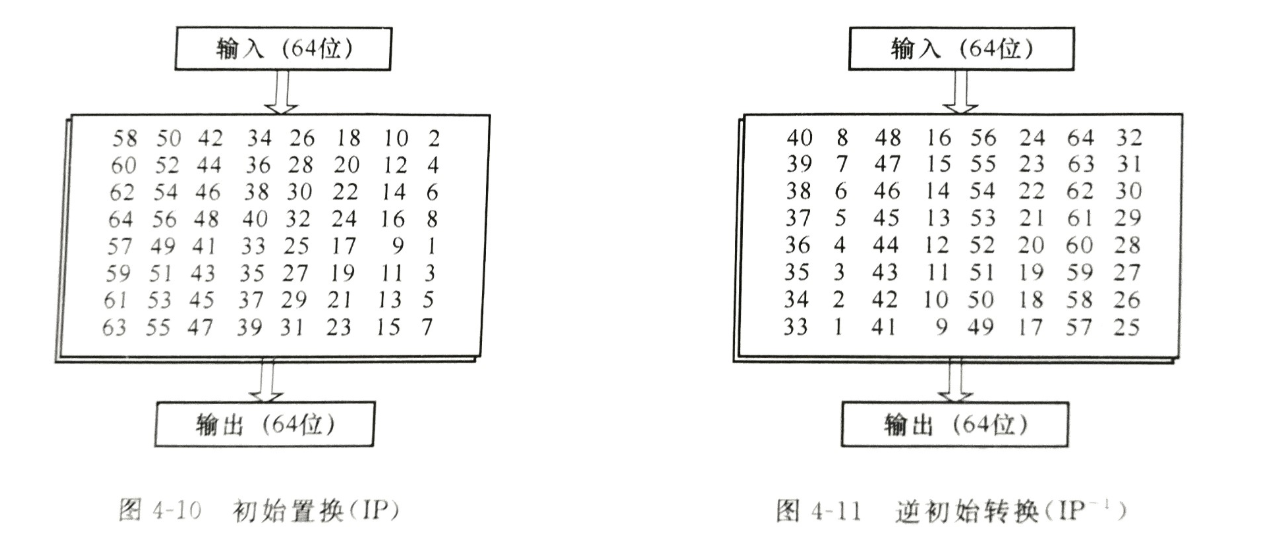
#IP盒处理
def ip_change(bin_str):
    res = ""
    for i in IP_table:
        res += bin_str[i-1]     #数组下标i-1
    return res


#IP逆盒处理
def ip_re_change(bin_str):
    res = ""
    for i in IP_re_table:
        res += bin_str[i-1]
    return res

F 函数

也称轮函数，包括四个过程：

  1. 扩展置换 ( E 盒 )
  2. 密钥加
  3. S 盒
  4. P 盒

下面，我们分别解释这几个过程。

1. 扩展置换

32 bit → 48 bit\

通过扩展置换，数据的右半部分 从 32 位扩展到 48 位。扩展置换改变了位的次序，重复了某些位。

image-20210112205546510
image-20210112205546510

目的：让明文的 1 位可能影响到密文的 2 位，从而快速实现了雪崩效应。（结合 S 盒）

#E盒置换
def e_key(bin_str):
    res = ""
    for i in E:
        res += bin_str[i-1]
    return res

2. 密钥加

48 bit ⊕ 48 bit → 48 bit\

E 盒输出与子密钥 Xor\ （逐位异或）。

Python 中，异或使用 ^ 运算符。因为我的处理方法是把字符转成对应的二进制（简单粗暴），所以我写了个封装 Xor\ 的函数：

#字符串异或操作
def str_xor(my_str1,my_str2):
    res = ""
    for i in range(0,len(my_str1)):
        xor_res = int(my_str1[i],10)^int(my_str2[i],10) #变成10进制是转化成字符串 2进制与10进制异或结果一样，都是1,0
        if xor_res == 1:
            res += '1'
        if xor_res == 0:
            res += '0'

    return res

3. 代换盒（S 盒）

48 bit → 32 bit\

目的是实现非线性代换，是 DES 中的唯一的非线性部分。

实际上是查表运算，8 个 S 盒对应把 48 位分成 8 个组（6 位一组）。

每个 S 盒的输入为 6 位，输出为 4 位。

image-20210112205534444
image-20210112205534444

利用了bin输出有可能不是4位str类型的值，所以才有下面的循环并且加上字符0

# S盒过程
def s_box(my_str):
    res = ""
    c = 0
    for i in range(0,len(my_str),6):
        now_str = my_str[i:i+6]
        row = int(now_str[0]+now_str[5],2)
        col = int(now_str[1:5],2)
        num = bin(S[c][row*16 + col])[2:]   #利用了bin输出有可能不是4位str类型的值，所以才有下面的循环并且加上字符0
        for gz in range(0,4-len(num)):
            num = '0'+ num
        res += num
        c  += 1
    return res

4. 置换盒（P 盒）

32 bit → 32 bit\

简单置换。

#P盒置换
def p_box(bin_str):
    res = ""
    for i in  P:
        res += bin_str[i-1]
    return res

运行结果

加密

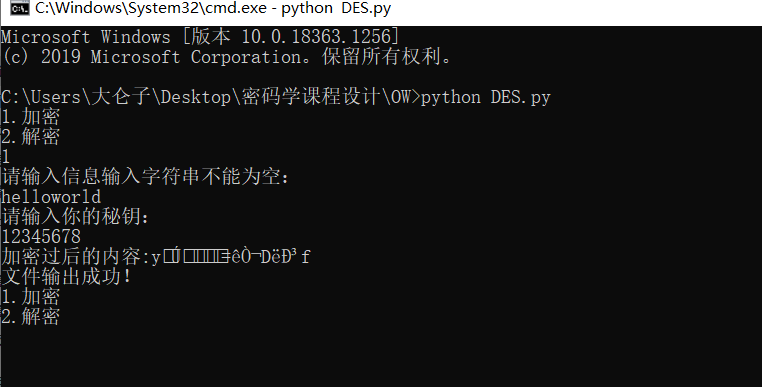
解密

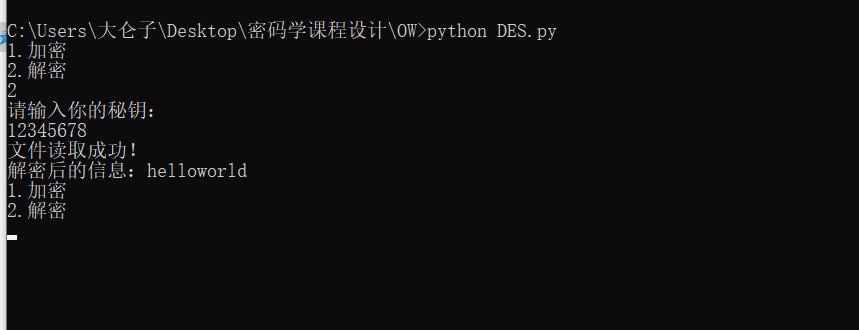
安全性分析

安全性争论：

  • S盒的设计准则还没有完全公开，人们仍然不知道S盒的构造中是否使用了进一步的设计准则
  • DES存在一些弱密钥和半弱密钥
  • DES的56位密钥无法抵抗穷举攻击
  • 代数结构存在互补对称性

弱密钥：

给定初始密钥𝐾生成子密钥时，将种子密钥分成两个部分，如果𝐾使得这两部分的每一部分的所有位置全为0或1，则经子密钥产生器产生的各个子密钥都相同，即𝐾1=𝐾2=…=𝐾16，则称密钥𝐾为弱密钥（共有4个）

若𝐾为弱密钥，则对任意的64比特信息有：

Ek(Ek(m))=m和Dk(Dk(m))=mEk(Ek(m))=m和Dk(Dk(m))=m

半弱密钥：

把明文加密成相同的密文，即存在两个不同的密钥𝑘和𝑘′,使得𝐸𝑘 (𝑚)=𝐸(𝑘^′ ) (𝑚)

具有下述性质：

若𝑘和𝑘′为一对弱密钥，𝑚为明文组，则有：

Ek′(Ek(m))=Ek(Ek′(m))=mEk′(Ek(m))=Ek(Ek′(m))=m

互补性：

对明文𝑚逐位取补，记为𝑚 ̅，密钥𝐾逐位取补，记为𝑘 ̅ ， 若𝑐=𝐸𝑘(𝑚)，则有𝑐 ̅=𝐸_𝑘 ̅ (𝑚 ̅) ，称为算法上的互补性

由算法中两次异或运算的配置决定：两次异或运算一次在S盒之前，一次在P盒置换之后

若对DES 的明文和密钥同时取补，则扩展运算E的输出和子密钥产生器的输出也都取补，因而经异或运算后的输出和未取补时的输出一样，即到达S盒的输入数据未变，输出自然也不变，但经第二个异或运算时，由于左边数据已取补，因而输出也就取补

互补性使DES在选择明文攻击下所需的工作量减半（2^55）

对选择的明文𝑚和𝑚 ̅ 加密后得到密文如下：

c1=Ek(m)c2=Ek(m−)c1=Ek(m)c2=Ek(m−)

由对称互补性可得

c−2=Ek−(m)c2−=Ek−(m)

所以对𝑚加密，如果密文为𝑐_1，则加密密钥为𝑘, 如果密文为(𝑐_2 ) ̅，则加密密钥为𝑘 ̅

差分分析法：

通过分析特定明文差对结果密文差的影响来获得可能性最大的密钥。这种攻击方法主要适用于攻击迭代分组密码，最初是针对DES提出的一种攻击方法，虽然差分攻击方法对破译16轮的DES不能提供一种实用的方法，但对破译轮数较低的DES是很成功的。

线性分析法：

寻找一个给定密码算法的有关明文比特、密文比特和密钥比特的有效线性近似表达式，通过选择充分多的明－密文对来分析密钥的某些比特，用这种方法破译DES比差分分析方法更有效。可用247个已知明文破译8－轮DES。

三重DES：

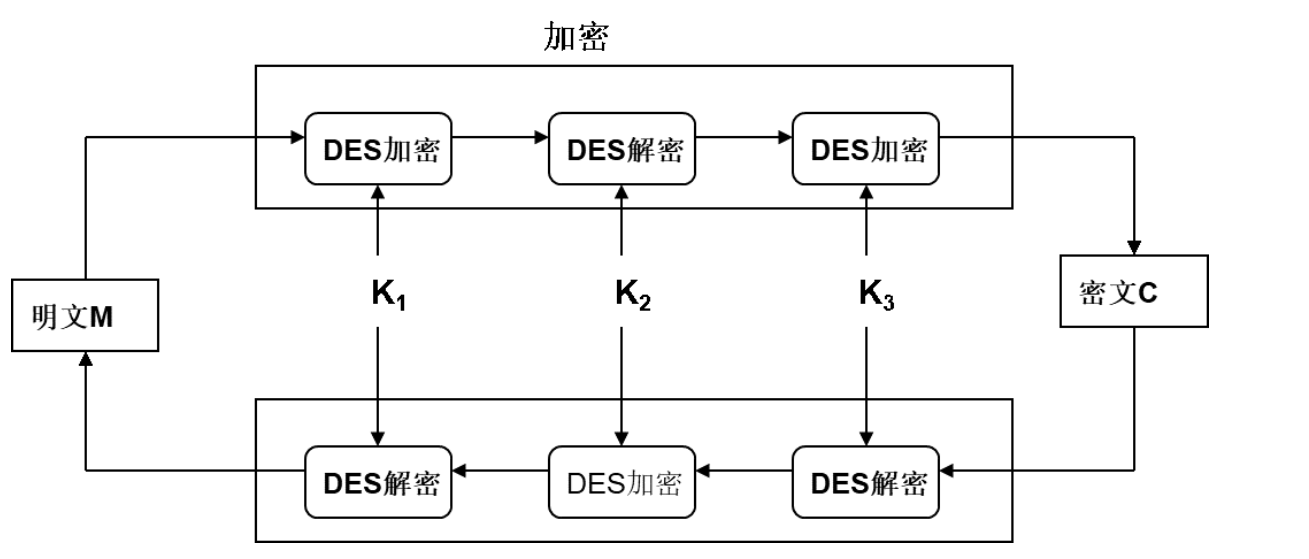
两密钥的3DES称为加密-解密-加密方案，简记为EDE(encrypt-decrypt-encrypt)

破译它的穷举密钥搜索量为2112 量级，用差分分析破译也要超过1035sup>量级。此方案仍有足够的安全性。

公钥密码RSA

RSA算法原理

  1. 密钥的生成

  • 选择两个大素数 𝑝和𝑞,（𝑝≠𝑞，需要保密，步骤4以后建议销毁）

  • 计算𝑛=𝑝×𝑞， (𝑛)=(𝑝－1)×(𝑞－1)

  • 选择整数 𝑒 使 ((𝑛)，𝑒) =1, 1<𝑒< (𝑛)

  • 计算𝑑，使𝑑=𝑒－1 𝑚𝑜𝑑 (𝑛),

    得到：公钥为{𝑒, 𝑛}； 私钥为{𝑑}

  1. 加密(用𝒆，𝒏)： 明文𝑀<𝑛， 密文𝐶=𝑀^𝑒 (𝑚𝑜𝑑 𝑛).
  2. 解密(用𝒅，𝒏)： 密文𝐶， 明文𝑀 =𝐶^𝑑 (𝑚𝑜𝑑 𝑛)

大素数生成

对于大整数的素性测试，一般用 Miller-Rabin 算法。它是一个基于概率的算法，是费马小定理（若 n 是一个素数，则 an-1 ≡ 1 (mod n) ）的一个改进。要测试 n 是否为素数，首先将 n−1 分解为 2sd 。在每次测试开始时，先随机选一个介于 [1,n−1] 的整数 a ，之后如果对所有的 r∈[0,s−1] ，若admodn≠1 且 a2rd mod n≠−1，则 n 是合数。否则，n 有 3/4 的概率为素数。增加测试的次数，该数是素数的概率会越来越高。这样，我们就可以给定位数 n 的情况下随机生成数，然后再用 Miller-Rabin 算法验证它是不是素数，若是，则就用它，否则再随机生成其他数字，循环。Python 脚本如下：

def miller_rabin(n, k=10):
    """
    用Miler-Rabin算法进行素性检验
    :param n: 被检验的数
    :param k: 检验的次数，默认为15次
    :return: 是否通过检验
    要测试n是否为素数,首先将n−1分解为(2^s)d
    在每次测试开始时,先随机选一个介于[1,n−1]的整数a,之后如果对所有的r∈[0,s−1] ,
    若a^d ≠1  (mod n)且 a^(2^rd)≠−1(mod n),则n是合数
    否则，n 有 3/4 的概率为素数,增加测试的次数,该数是素数的概率会越来越高。
    """
    # 偶数直接不通过
    if n % 2 == 0:
        return False
    s, d = 0, n - 1
    # 将p-1分解为(2**s)d
    while d % 2 == 0:
        s += 1
        d //= 2
    # 进行k次检验566++3.+6
    for i in range(k):
        # 每次测试时,随机选取一个[1,n-1]的整数a
        a = randint(1, n - 1)
        x = pow(a, d, n)  # x = a**d mod(n)
        # 如果a**d(mod n)=1,说明当次检验通过(不是合数),进行下一轮检验
        if x == 1 or x == n - 1:
            continue
        else:
            flag = 0
            # 对所有的r∈[0, s-1],判断a**((2**r)*d) (mod n)是否等于-1，
            for r in range(s):
                # x**pow(2,r) == a**d**pow(2,r)
                x = pow(x, 2, n)
                if x == n - 1:
                    flag = 1
                    break
            # 若a**d≠1(mod n)且a**pow(2,r)**≠
            if flag == 0:
                return False
    return True

带模的幂运算

原理：模重复平方运算，Python 代码如下：

def fast_mod(x, n, p):
    x = x % p
    res = 1
    while n!=0:
        if n & 1:
            res = (res * x) % p
        n >>= 1     # 相当于 n //= 2
        x = (x * x) % p
    return res

求逆运算

扩展欧几里得法

def extended_gcd(a, b):
    """
    扩展的欧几里得算法计算gcd的最大公因子g以及x和y,满足g=ax+by
    递归式的推导过程:
    ax₁ + by₁ = gcd(a,b)
    bx₂ + (a%b)y₂ = gcd(b,a%b)
    ∵ gcd(a,b) = gcd(b,a%b) 且 a%b = a - (a//b)*b
    ∴ bx₂ + (a%b)y₂
     = bx₂ + [a - (a//b)*b]y₂
     = ay₂ + bx₂ - (a//b)by₂
     = ay₂ + b[x₂ - (a//b)y₂]
     = ax₁ + by₁
     ∴待定系数法得:x₁ = y₂, y₁ = x₂ - (a//b)y₂
     递归终止条件: 当b = 0, gcd(a,b) = a, 此时 x = 1,y = 0
    :return: (g,s,t)
    """
    if b == 0:
        return a, 1, 0
    else:
        g, x, y = extended_gcd(b, a % b)  # 先得到更里层的x₂,y₂,
        return g, y, x - (a // b) * y  # 再根据得到的x₂,y₂,计算x₁,y₁


def mod_inverse(a, m):
    """
    计算模逆,即a**-1 (mod m)
    :param a: 底数
    :param m: 模数
    :return: 逆元
    """
    g, x, y = extended_gcd(a, m)  # ax + my = 1
    # 若a,m不互素,则不可逆
    if g != 1:
        raise Exception(str(a) + ' is not invertible!')
    else:
        return x % m

运行结果

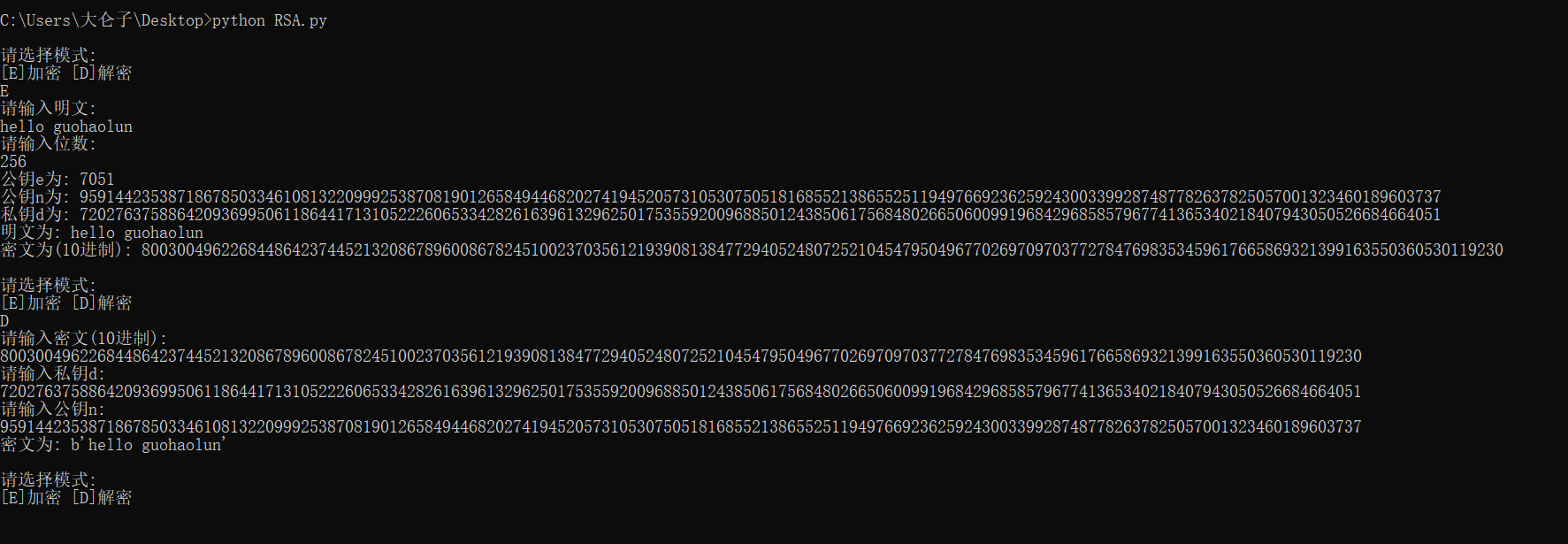
安全性分析

RSA的安全性依赖于大数分解问题，目前，还未能从数学上证明由𝑐和𝑒计算出𝑚一定需要分解𝑛，然而，如果新方法能使密码分析者推算出𝑑，它也就成为大数分解的一个新方法

非对称加密算法中 1024 bit 密钥的强度相当于对称加密算法 80bit 密钥的强度。但是，从效率上，密钥长度增长一倍，公钥操作所需时间增加约 4 倍，私钥操作所需时间增加约 8 倍，公私钥生成时间约增长16倍。所以，我们要权衡一下效率和安全性。一般来说， 1024 bit 只能用于加密 最多117 字节的明文。

低加密指数攻击：

为了使加密高效，一般希望选取较小的加密指数 ee ，但是 ee 不能太小，否则容易遭到低加密指数攻击。

假设用户使用的密钥 e=3e=3 。考虑到加密关系满足：

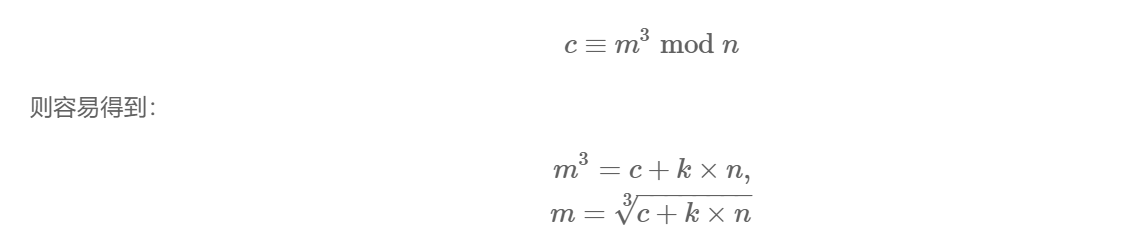
低加密指数广播攻击：

还有一种情况是如果给 k 个用户发的都是同个低加密指数比如 e=3 ，在不同的模数 n1.n2,n3下 ，可由 CRT（中国剩余定理） 解出 m3 ，从而直接开三次根解出 m。

共模攻击：

场景：n 相同（让多个用户使用相同的模数 n ），但他们的公私钥对不同。这样，我们可以在已知 n,e1,e2,c1,c2 的情况下解出 m 。过程如下：

其实有个隐形的前提条件是：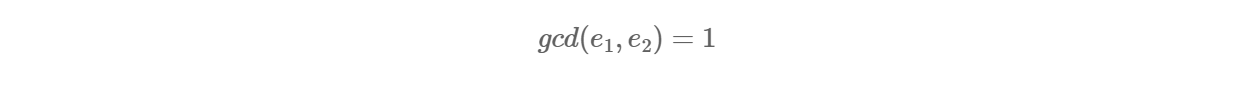

存在 s1,s2 使得：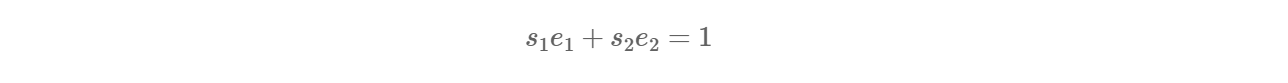

又由 RSA 定义可知：

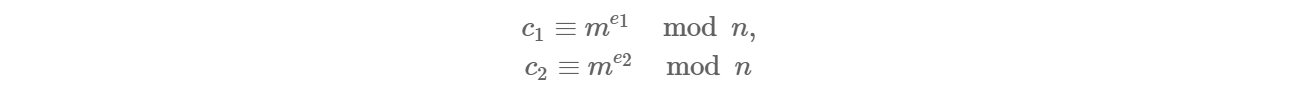
可得出：

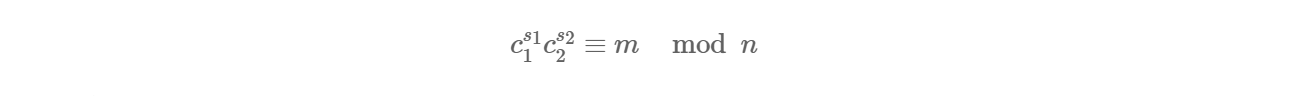
这样，我们仅需要使用扩展欧几里得算法求出 s1,s2s1,s2 便可解出明文。

MD5加密

概述

Hash，一般翻译做散列、杂凑，或音译为哈希，是把任意长度的输入(又叫做预映射)通过散列算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是说，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是是将任意长度的输入变换为固定长度的输出的不可逆的单向密码体制。

MD5(Message-Digest Algorithm,信息摘要算法)，是由美国著名密码学家Rivest设计的一种密码散列函数，可以将长度小于264比特的消息，按512比特的分组单位进行处理，输出一个128比特的消息摘要。

MD5具有Hash函数的所有特性。

​ ①压缩性。无论输入的明文多长，计算出来的MD5值长度固定为128位。

​ ②易计算性。由原数据容易计算出MD5值 。

​ ③抗碰撞性。知道明文和MD5值，很难找到相同MD5值相同的明文。

​ ④抗修改性。即便修改一个字节，计算出来的MD5值也会存在极大差异

​ MD5是在MD4基础上发展而来的，虽然比MD4稍慢，但更安全，实现了更快的雪崩效应，在实际应用中更受欢迎。

​ 散列函数的安全性主要体现在其良好的单向性和对碰撞的有效避免。由于散列变换是一种压缩变换，输入和输出长度相差极大啊，很难通过输出来确定 输入。但是，散列函数经常被用于数据改动检测，如果一个合法消息和一个非法消息能够碰撞，攻击就可以用合法消息生成散列值，再以非法消息作为该散列值的对应消息进行欺骗，且是他人无法识别。所以，对于Hash函数的攻击，攻击者的主要目标不是恢复原始明文，而是用相同散列值的非法消息来替代合法消息进行伪造和欺骗。

​ 对于MD5的碰撞研究，王小云教授做出了突破性的贡献，她的研究成果可以概括为：对于给定的M1，可以比较快速地找到M2，使得H(M1)=H(M2)。在2004年发表的论文中，她在IBM P690上用了一个小时左右就找了这样的一个碰撞，放到现在的计算机上面，这个时间会更短。所以，如果是要求高度保密的场所，比如说军工之类，MD5已经不安全了，应更换为更安全的Hash算法；但对于民用来说，一般没有人有能承受那么大计算量的设备，在一些不重要的认证上面仍可使用。

MD5算法原理

消息填充

  • 使消息长度模512=448如果消息长度模512恰等于448，增加512个填充比特。即填充的个数为1~512，填充方法：第1比特为1，其余全部为0
  • 将消息长度转换为64比特的数值，如果长度超过64比特所能表示的数据长度，值保留最后64比特添加到填充数据后面，使数据为512比特的整数倍
  • 512比特按32比特分为16组

注：64位数据长度存储的时候是小端序

初始化链接变量

使用4个32位的寄存器A， B，C， D存放4个固定的32位整型参数，用于第一轮迭代，这里需要注意的是，寄存器的值要转化为小端序。

A=0x01234567 B=0x89abcdef C=0xfedcba98 D=0x76543210

分组处理

与分组密码分组处理相似，有4轮步骤，将512比特的消息分组平均分为16个子分组，每个子分组有32比特，参与每一轮的的16步运算，每步输入是4个32比特的链接变量和一个32位的的消息子分组，经过这样的64步之后得到4个寄存器的值分别与输入的链接变量进行模加。

步函数

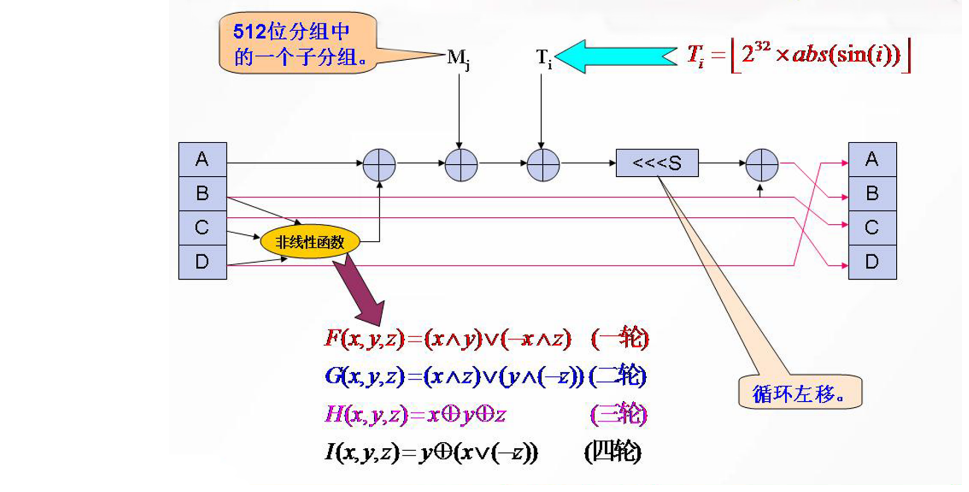
image-20210112205456498
image-20210112205456498

该函数包括 4 轮，每轮 16 步，上一步的链接变量 D, B, C 直接赋值给下一步的链接变量 A, C, D。

A 先和非线性函数的结果加一下，结果再和 M[j] 加一下，结果再和 T[i] 加一下，结果再循环左移 s 次，结果再和原来的 B 加一下，最后的得到新 B。

非线性函数：

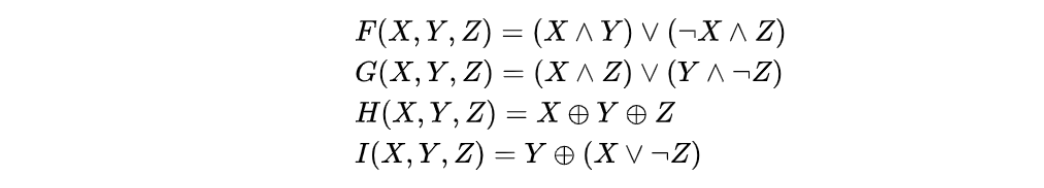
image-20210112205446350
image-20210112205446350

代码实现

消息填充

# 对消息进行填充
def message_padding(m):
    # 计算附加的64为长度(小端序表示)
    len_padding = bin2little(bin(len(m))[2:].zfill(64))
    m += '1'
    while len(m) % 512 != 448:
        m += '0'
    return m + len_padding

初始化链接变量

# 初始链接变量(小端序表示)
IV_A, IV_B, IV_C, IV_D = (0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476)

分组处理及步函数

# 压缩函数(对每个512bit分组进行处理)
def compress_func(a, b, c, d, m):
    """
    压缩函数函数,对每512bit得分组进行处理,包括4轮,每轮16步
    :param a, b, c, d:  输入链接变量(即前一个分组的输出链接变量)
    :param m: 512bit的消息分组
    :return: A,B,C,D 输出链接变量
    """
    # 对每一分组的初始链接变量进行备份
    A, B, C, D = a, b, c, d
    # 将512bit分为16组,每组32bit
    m_list_32 = re.findall(r'.{32}', m)
    # 每个分组经过4轮函数
    for round_index in range(4):
        # 每轮有16步
        for step_index in range(16):
            # 对每一步的链接变量进行备份
            AA, BB, CC, DD = A, B, C, D
            # 每一轮选择不同的非线性函数
            if round_index == 0:
                func_out = F(B, C, D)
            elif round_index == 1:
                func_out = G(B, C, D)
            elif round_index == 2:
                func_out = H(B, C, D)
            else:
                func_out = I(B, C, D)
            A, C, D = D, B, C
            # B模加非线性函数的输出
            B = mod_add(AA, func_out)
            # 模加消息分组(注意为大端序)
            B = mod_add(B, int(bin2little(m_list_32[M_index_[round_index][step_index]]), 2))
            # print(type(B))
            # 模加伪随机常数
            B = mod_add(B, T(16 * round_index + step_index + 1))
            # 循环左移s位
            B = rol(B, shift_[round_index][step_index])
            # 模加BB
            B = mod_add(B, BB)
        #     print(str(16 * round_index + step_index + 1).zfill(2), end=" ")
        #     print(hex(A).replace("0x", "").replace("L", "").zfill(8), end=" ")
        #     print(hex(B).replace("0x", "").replace("L", "").zfill(8), end=" ")
        #     print(hex(C).replace("0x", "").replace("L", "").zfill(8), end=" ")
        #     print(hex(D).replace("0x", "").replace("L", "").zfill(8))
        # print("*" * 38)
    # 与该分组的初始链接变量异或
    A = mod_add(A, a)
    B = mod_add(B, b)
    C = mod_add(C, c)
    D = mod_add(D, d)

    return A, B, C, D

运行结果

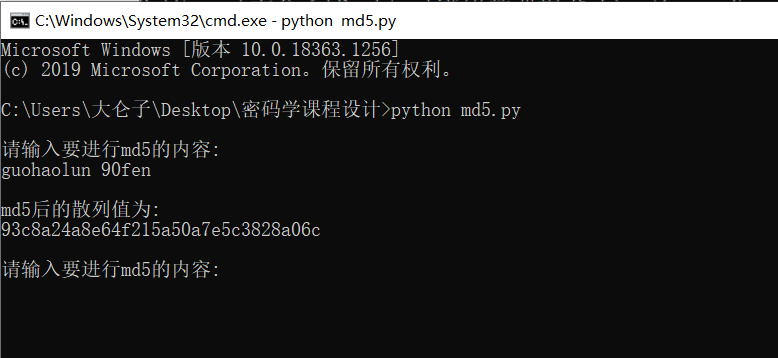
找一个在线加密的网站验证一下

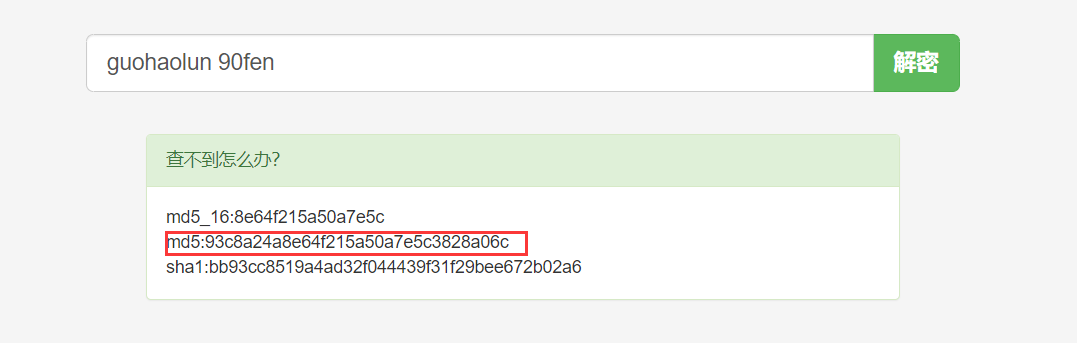
安全性分析

攻击者的主要目标不是恢复原始的明文，而是用非法消息替代合法消息进行伪造和欺骗，对哈希函数的攻击也是寻找碰撞的过程。

基本攻击方法：

（1）穷举攻击：能对任何类型的Hash函数进行攻击

最典型方法是“生日攻击”：给定初值𝐻0=H(M)，寻找𝑀’≠ 𝑀，使ℎ(𝑀’)= 𝐻0

（2）密码分析法：依赖于对Hash函数的结构和代数性质分析，采用针对Hash函数弱性质的方法进行攻击。这类攻击方法有中间相遇攻击、修正分组攻击和差分分析等

MD5算法中，输出的每一位都是输入的每一位的函数，逻辑函数F、G、H、I的复杂迭代使得输出对输入的依赖非常小

但Berson证明，对单轮的MD5算法，利用差分分析，可以在合理时间内找出碰撞的两条消息

MD5算法抗密码分析的能力较弱，生日攻击所需代价是试验264个消息

2004年8月17日，在美国加州圣巴巴拉召开的美密会（Crypto2004）上，中国的王小云、冯登国、来学嘉、于红波4位学者宣布，只需1小时就可找出MD5的碰撞（利用差分分析）