祥云杯复现

Crypto

Exposure

题目考点：

dp高位泄露

题目：

Do you know how to rsa?
from Crypto.Util.number import *
import gmpy2

p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
phi = (p - 1) * (q - 1)
e = 7621
d = gmpy2.invert(e, phi)

flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"
c = pow(bytes_to_long(flag), e, n)

dp = d % (p - 1)
print(dp >> 200)
print(c, e, n)

'''
dp>>200 = 1153696846823715458342658568392537778171840014923745253759529432977932183322553944430236879985
c = 46735962204857190520476434898881001530665718155698898882603422023484998388668858692912250418134186095459060506275961050676051693220280588047233628259880712415593039977585805890920089318643002597837000049626154900908543384761210358835843974072960080857150727010985827690190496793207012355214605393036388807616
e = 7621
n = 140376049134934822153964243403031201922239588054133319056483413311963385321279682186354948441840374124640187894619689719746347334298621083485494086361152915457458004998419817456902929318697902819798254427945343361548635794308362823239150919240307072688623000747781103375481834571274423004856276841225675241863
'''
1234567891011121314151617181920212223

解题
参考文章：https://github.com/pcw109550/write-up/tree/master/2019/KAPO/Lenstra-Lenstra-Lovasz

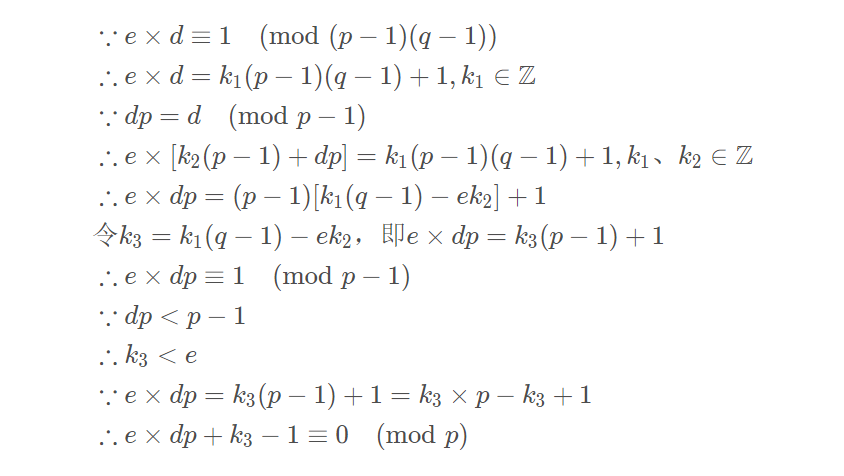
这道题知道secret = dp>>200，即已知dp的高位恢复出dp。

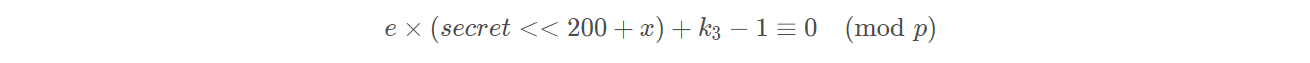
#sage
#dp高位泄露攻击，这里泄露了(secret=dp>>200)
secret = 1153696846823715458342658568392537778171840014923745253759529432977932183322553944430236879985
e = 7621
n = 140376049134934822153964243403031201922239588054133319056483413311963385321279682186354948441840374124640187894619689719746347334298621083485494086361152915457458004998419817456902929318697902819798254427945343361548635794308362823239150919240307072688623000747781103375481834571274423004856276841225675241863

F.<x> = PolynomialRing(Zmod(n))
d = inverse_mod(e, n)
for k in range(1, e):
	# 这里爆破得到 k=1237
	print('k =',k)
	f = (secret << 200) + x + (k - 1) * d
	x0 = f.small_roots(X=2 ** (200 + 1), beta=0.44, epsilon=1/32)
	if len(x0) != 0:
		dp = x0[0] + (secret << 200)
		for i in range(2, e):
			p = (e * Integer(dp) - 1 + i) // i
			if n % p == 0:
				break
		if p < 0:
			continue
		else:
			print('p =',p)
			print('dp =',dp)
			break
12345678910111213141516171819202122232425

整合脚本，获取flag。

#sage
secret = 1153696846823715458342658568392537778171840014923745253759529432977932183322553944430236879985
c = 46735962204857190520476434898881001530665718155698898882603422023484998388668858692912250418134186095459060506275961050676051693220280588047233628259880712415593039977585805890920089318643002597837000049626154900908543384761210358835843974072960080857150727010985827690190496793207012355214605393036388807616
e = 7621
n = 140376049134934822153964243403031201922239588054133319056483413311963385321279682186354948441840374124640187894619689719746347334298621083485494086361152915457458004998419817456902929318697902819798254427945343361548635794308362823239150919240307072688623000747781103375481834571274423004856276841225675241863

[n, secret, c] = list(map(Integer, [n, secret, c]))

def facorize(e, dp):
	for i in range(2, e):
		p = (e * dp - 1 + i) // i
		if n % p == 0:
			return p
	return -1

def recover(secret):
	F.<x> = PolynomialRing(Zmod(n))
	d = inverse_mod(e, n)
	for k in range(1235, e):
		print('k =',k)
		f = (secret << 200) + x + (k - 1) * d
		x0 = f.small_roots(X=2 ** (200 + 1), beta=0.44, epsilon=1/32)
		if len(x0) != 0:
			dp = x0[0] + (secret << 200)
			p = facorize(e, Integer(dp))
			if p < 0:
				continue
			else:
				return p, dp

if __name__ == "__main__":
	p, dp = recover(secret)
	q = n // p
	assert p * q == n
	phi = (p - 1) * (q - 1)
	d = inverse_mod(e, phi)
	print('p =',p)
	print('q =',q)
	m = pow(c, d, n)
	flag = bytes.fromhex(hex(m)[2:])
	print(flag)
1234567891011121314151617181920212223242526272829303132333435363738394041

more_calc

题目：

maybe u need more cpu
import gmpy2
from Crypto.Util.number import *

flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"

p = getStrongPrime(2048)
for i in range(1, (p+1)//2):
    s += pow(i, p-2, p)
s = s % p
q = gmpy2.next_prime(s)
n = p*q
e = 0x10001
c = pow(bytes_to_long(flag), e, n)
print(p)
print(c)
'''
p = 27405107041753266489145388621858169511872996622765267064868542117269875531364939896671662734188734825462948115530667205007939029215517180761866791579330410449202307248373229224662232822180397215721163369151115019770596528704719472424551024516928606584975793350814943997731939996459959720826025110179216477709373849945411483731524831284895024319654509286305913312306154387754998813276562173335189450448233216133842189148761197948559529960144453513191372254902031168755165124218783504740834442379363311489108732216051566953498279198537794620521800773917228002402970358087033504897205021881295154046656335865303621793069
c = 350559186837488832821747843236518135605207376031858002274245004287622649330215113818719954185397072838014144973032329600905419861908678328971318153205085007743269253957395282420325663132161022100365481003745940818974280988045034204540385744572806102552420428326265541925346702843693366991753468220300070888651732502520797002707248604275755144713421649971492440442052470723153111156457558558362147002004646136522011344261017461901953583462467622428810167107079281190209731251995976003352201766861887320739990258601550606005388872967825179626176714503475557883810543445555390014562686801894528311600623156984829864743222963877167099892926717479789226681810584894066635076755996423203380493776130488170859798745677727810528672150350333480506424506676127108526488370011099147698875070043925524217837379654168009179798131378352623177947753192948012574831777413729910050668759007704596447625484384743880766558428224371417726480372362810572395522725083798926133468409600491925317437998458582723897120786458219630275616949619564099733542766297770682044561605344090394777570973725211713076201846942438883897078408067779325471589907041186423781580046903588316958615443196819133852367565049467076710376395085898875495653237178198379421129086523
'''
12345678910111213141516171819

解题：

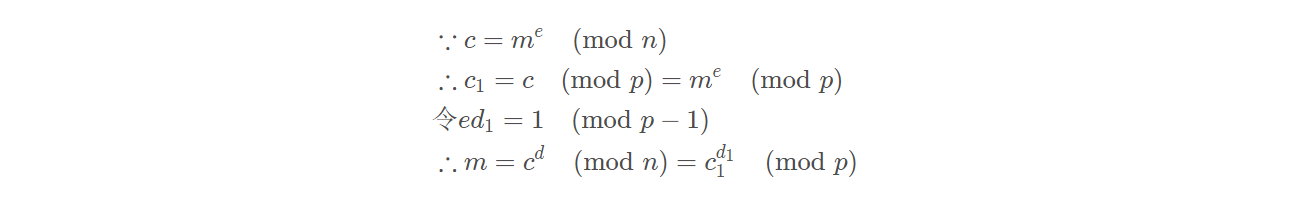
import gmpy2

p=27405107041753266489145388621858169511872996622765267064868542117269875531364939896671662734188734825462948115530667205007939029215517180761866791579330410449202307248373229224662232822180397215721163369151115019770596528704719472424551024516928606584975793350814943997731939996459959720826025110179216477709373849945411483731524831284895024319654509286305913312306154387754998813276562173335189450448233216133842189148761197948559529960144453513191372254902031168755165124218783504740834442379363311489108732216051566953498279198537794620521800773917228002402970358087033504897205021881295154046656335865303621793069
c=350559186837488832821747843236518135605207376031858002274245004287622649330215113818719954185397072838014144973032329600905419861908678328971318153205085007743269253957395282420325663132161022100365481003745940818974280988045034204540385744572806102552420428326265541925346702843693366991753468220300070888651732502520797002707248604275755144713421649971492440442052470723153111156457558558362147002004646136522011344261017461901953583462467622428810167107079281190209731251995976003352201766861887320739990258601550606005388872967825179626176714503475557883810543445555390014562686801894528311600623156984829864743222963877167099892926717479789226681810584894066635076755996423203380493776130488170859798745677727810528672150350333480506424506676127108526488370011099147698875070043925524217837379654168009179798131378352623177947753192948012574831777413729910050668759007704596447625484384743880766558428224371417726480372362810572395522725083798926133468409600491925317437998458582723897120786458219630275616949619564099733542766297770682044561605344090394777570973725211713076201846942438883897078408067779325471589907041186423781580046903588316958615443196819133852367565049467076710376395085898875495653237178198379421129086523
e=0x10001
c1=c%p
d1=gmpy2.invert(e,p-1)
m=pow(c1,d1,p)
flag = bytes.fromhex(hex(m)[2:])
print(flag)
12345678910

RSAssss

题目考点：

费马因式分解

题目：

more factors,more strong
from Crypto.Util.number import *
from gmpy2 import next_prime

p = getPrime(512)
q = getPrime(512)

n = p * q * next_prime(p) * next_prime(q)
e = 0x10001

flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"
cipher = pow(bytes_to_long(flag), e, n)

print(n, cipher)

'''
n = 8030860507195481656424331455231443135773524476536419534745106637165762909478292141556846892146553555609301914884176422322286739546193682236355823149096731058044933046552926707682168435727800175783373045726692093694148718521610590523718813096895883533245331244650675812406540694948121258394822022998773233400623162137949381772195351339548977422564546054188918542382088471666795842185019002025083543162991739309935972705871943787733784491735500905013651061284020447578230135075211268405413254368439549259917312445348808412659422810647972872286215701325216318641985498202349281374905892279894612835009186944143298761257
cipher = 3304124639719334349997663632110579306673932777705840648575774671427424134287680988314129312593361087606243819528298610131797078262351307396831985397555390640151391138633431951746748156610463582479645561779194981806129898009876517899450840875569675976765155608446799203699927448835004756707151281044859676695533373755798273892503194753948997947653100690841880925445059175494314198605475023939567750409907217654291430615102258523998394231436796902635077995829477347316754739938980814293304289318417443493019704073164585505217658570214989150175123757038125380996050761572021986573934155470641091678664451080065719261207
'''
123456789101112131415161718

解题：
参考文章：https://github.com/pcw109550/write-up/tree/master/2019/ISITDTU/Easy_RSA_2

exp：

from Cryptodome.Util.number import *
from gmpy2 import *

e = 0x10001
n = 8030860507195481656424331455231443135773524476536419534745106637165762909478292141556846892146553555609301914884176422322286739546193682236355823149096731058044933046552926707682168435727800175783373045726692093694148718521610590523718813096895883533245331244650675812406540694948121258394822022998773233400623162137949381772195351339548977422564546054188918542382088471666795842185019002025083543162991739309935972705871943787733784491735500905013651061284020447578230135075211268405413254368439549259917312445348808412659422810647972872286215701325216318641985498202349281374905892279894612835009186944143298761257
c = 3304124639719334349997663632110579306673932777705840648575774671427424134287680988314129312593361087606243819528298610131797078262351307396831985397555390640151391138633431951746748156610463582479645561779194981806129898009876517899450840875569675976765155608446799203699927448835004756707151281044859676695533373755798273892503194753948997947653100690841880925445059175494314198605475023939567750409907217654291430615102258523998394231436796902635077995829477347316754739938980814293304289318417443493019704073164585505217658570214989150175123757038125380996050761572021986573934155470641091678664451080065719261207

def fermat_factorization(n):
	factor_list = []
	get_context().precision = 2048
	x = int(sqrt(n))

	while True:
		x += 1
		y2 = x ** 2 - n
		if is_square(y2):
			#print('x = ',x)
			y2 = mpz(y2)
			get_context().precision = 2048
			y = int(sqrt(y2))
			factor_list.append([x+y, x-y])
		if len(factor_list) == 2:
			break
	return factor_list

def main():
	factor_list = fermat_factorization(n)
	#print(factor_list)
	[X1, Y1] = factor_list[0]
	[X2, Y2] = factor_list[1]
	assert X1 * Y1 == n
	assert X2 * Y2 == n
	p1 = gcd(X1, X2)
	q1 = X1 // p1
	p2 = gcd(Y1, Y2)
	q2 = Y1 // p2
	#print('p1 =',p1)
	#print('p2 =',p2)
	#print('q1 =',q1)
	#print('q2 =',q2)

	phi = (p1 - 1) * (q1 - 1) * (p2 - 1) * (q2 - 1)
	d = inverse(e, phi)
	flag = long_to_bytes(pow(c, d, n))
	print(flag)

if __name__ == "__main__":
	main()
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

simpleRSA

题目考点：

低解密指数攻击

题目：

Familiar and simple rsa
from Crypto.Util.number import *
import gmpy2

p, q, r = [getPrime(512) for i in range(3)]
n = p * q * r
phi = (p - 1) * (q - 1) * (r - 1)
d = getPrime(256)
e = gmpy2.invert(d , phi)

flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"

c = pow(bytes_to_long(flag), e, n)

print(e, n)
print(c)

'''
e = 1072295425944136507039938677101442481213519408125148233880442849206353379681989305000570387093152236263203395726974692959819315410781180094216209100069530791407495510882640781920564732214327898099944792714253622047873152630438060151644601786843683746256407925709702163565141004356238879406385566586704226148537863811717298966607314747737551724379516675376634771455883976069007134218982435170160647848549412289128982070647832774446345062489374092673169618836701679
n = 1827221992692849179244069834273816565714276505305246103435962887461520381709739927223055239953965182451252194768935702628056587034173800605827424043281673183606478736189927377745575379908876456485016832416806029254972769617393560238494326078940842295153029285394491783712384990125100774596477064482280829407856014835231711788990066676534414414741067759564102331614666713797073811245099512130528600464099492734671689084990036077860042238454908960841595107122933173
c = 1079929174110820494059355415059104229905268763089157771374657932646711017488701536460687319648362549563313125268069722412148023885626962640915852317297916421725818077814237292807218952574111141918158391190621362508862842932945783059181952614317289116405878741758913351697905289993651105968169193211242144991434715552952340791545323270065763529865010326192824334684413212357708275259096202509042838081150055727650443887438253964607414944245877904002580997866300452
'''
123456789101112131415161718192021

解题：

参考lazzzaro师傅的文章。

exp：

from Cryptodome.Util.number import long_to_bytes
e = 1072295425944136507039938677101442481213519408125148233880442849206353379681989305000570387093152236263203395726974692959819315410781180094216209100069530791407495510882640781920564732214327898099944792714253622047873152630438060151644601786843683746256407925709702163565141004356238879406385566586704226148537863811717298966607314747737551724379516675376634771455883976069007134218982435170160647848549412289128982070647832774446345062489374092673169618836701679
n = 1827221992692849179244069834273816565714276505305246103435962887461520381709739927223055239953965182451252194768935702628056587034173800605827424043281673183606478736189927377745575379908876456485016832416806029254972769617393560238494326078940842295153029285394491783712384990125100774596477064482280829407856014835231711788990066676534414414741067759564102331614666713797073811245099512130528600464099492734671689084990036077860042238454908960841595107122933173
c = 1079929174110820494059355415059104229905268763089157771374657932646711017488701536460687319648362549563313125268069722412148023885626962640915852317297916421725818077814237292807218952574111141918158391190621362508862842932945783059181952614317289116405878741758913351697905289993651105968169193211242144991434715552952340791545323270065763529865010326192824334684413212357708275259096202509042838081150055727650443887438253964607414944245877904002580997866300452

#连分数展开算法
def lf(x,y):
	arr=[]
	while y:
		arr+=[x//y]
		x,y=y,x%y
	return arr
#渐进分数算法
def jj(k):
	x=0
	y=1
	for i in k[::-1]:
		x,y=y,x+i*y
	return (y,x)
data=lf(e,n)

for x in range(1,len(data)+1):
	data1=data[:x]
	d = jj(data1)[1]
	m = pow(c,d,n)
	flag = long_to_bytes(m)
	if b'flag{' in flag:
		print(flag)
		break

RE

RE1

通过逆向发现 flag 的每一位都采用相同的加密方式，然后会在函数末尾判断，所以直接写一
个 gdb 脚本爆破明文对应密文的关系即可

gdb 脚本：

b *(0x8000000 + 0x18096)
python f = open('log','w+')
set $ipx = 0x20
r < test_input
while ($ipx < 0x80)
set *(char*)$rdi = $ipx
python f.write(gdb.execute('p $ipx', to_string=True))
set $pc=$rebase(0x810)
c
python s = gdb.execute('x/bx $rdi', to_string=True)
python f.write(s)
python f.flush()
set $ipx=$ipx+1
end
s = {32: 0xd8,33: 0xd9,34: 0xda,35: 0xdb,36: 0xdc,37: 0xdd,38: 0xde,39: 0xdf,40: 0xe0,41: 0xe1,42: 0xe2,43:
0xe3,44: 0xe4,45: 0xe5,46: 0xe6,47: 0xe7,48: 0xe8,49: 0xe9,50: 0xea,51: 0xeb,52: 0xec,53: 0xed,54: 0xee,55:
0xef,56: 0xf0,57: 0xf1,58: 0xf2,59: 0xf3,60: 0xf4,61: 0xf5,62: 0xf6,63: 0xf7,64: 0xf8,65: 0xf9,66: 0xfa,67:
0xfb,68: 0xfc,69: 0xfd,70: 0xfe,71: 0xff,72: 0x00,73: 0x01,74: 0x02,75: 0x03,76: 0x04,77: 0x05,78: 0x06,79:
0x07,80: 0x08,81: 0x09,82: 0x0a,83: 0x0b,84: 0x0c,85: 0x0d,86: 0x0e,87: 0x0f,88: 0x10,89: 0x11,90: 0x12,91:
0x13,92: 0x14,93: 0x15,94: 0x16,95: 0x17,96: 0x18,97: 0x19,98: 0x1a,99: 0x1b,100: 0x1c,101: 0x1d,102:
0x1e,103: 0x1f,104: 0x20,105: 0x21,106: 0x22,107: 0x23,108: 0x24,109: 0x25,110: 0x26,111: 0x27,112:
0x28,113: 0x29,114: 0x2a,115: 0x2b,116: 0x2c,117: 0x2d,118: 0x2e,119: 0x2f,120: 0x30,121: 0x31,122:
0x32,123: 0x33,124: 0x34,125: 0x35,126: 0x36,127: 0x37}
enc_flag =
[0x0EB,0x0F1,0x19,0x0E8,0x1E,0x1E,0x0F0,0x0EC,0x0EF,0x1E,0x0E9,0x1E,0x0EC,0x0EC,0x0E8,0x0EC,0x19,
0x19,0x0EE,0x1B,0x0EF,0x0EF,0x0EC,0x0EA,0x1C,0x0EA,0x0E8,0x0EB,0x0EE,0x0EB,0x1D,0x0F1]
for i in enc_flag:
for j in xrange(0x20,0x80):
if s[j] == i:
res += chr(j)
break