上海赛复现

RE

RE1 真正的Babyre

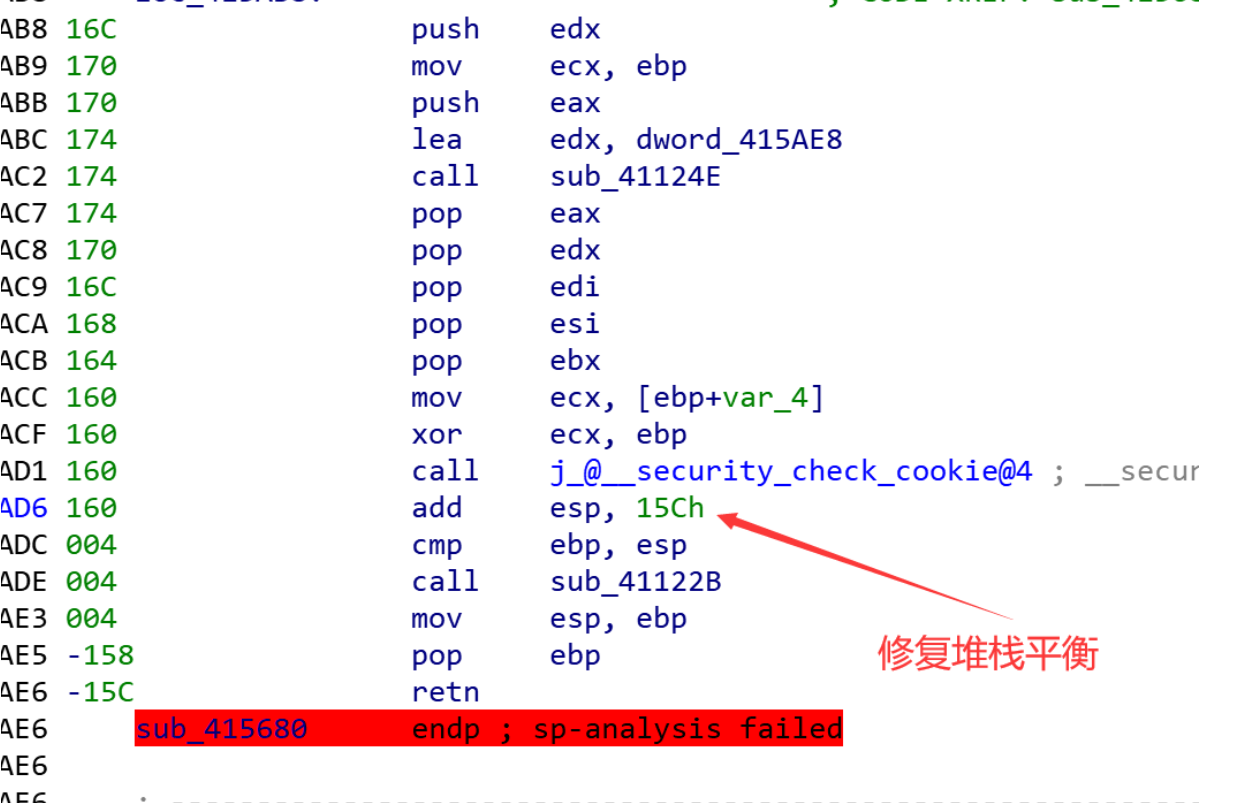
首先定位字符串，函数堆栈不平衡，首先修复堆栈不平衡问题。F5，寻找主逻辑。IDA启动调试，处理掉case3处的反调试。

dump出关键对比数据：

cipher=[0x1F, 0x18, 0x0F, 0xFA, 0xB8, 0x63, 0x64, 0x89, 0x18, 0x68, 

 0x7C, 0x19, 0x14, 0x2D, 0x7D, 0x58, 0x00, 0x1E, 0x54, 0x6A, 

 0x41, 0x3C, 0x36, 0x3E, 0x56, 0x13, 0x04, 0x3B, 0x2E, 0x4B, 

 0x79, 0x43, 0x7A, 0x22, 0x45, 0x6E, 0x3A, 0x75, 0x26, 0xC8, 

 0xC0, 0x8E]
table=[9, 2, 7, 8, 6, 9, 11, 10, 4, 11, 12, 4, 7, 7, 10, 4, 3, 9, 4, 6, 3, 12, 11, 13, 
4, 10, 7, 7, 2, 6, 6, 12, 9, 14, 7, 8, 11, 13, 14, 12, 4,7]
table2=[13, 8, 12, 10, 3, 9, 5, 12, 13, 11, 12, 7, 6, 10, 8, 9, 13, 8, 5, 10, 7, 
13, 4, 13, 2, 12, 10, 12, 9, 7, 14, 5, 11, 7, 13, 7, 13, 11, 5, 14, 6, 10]

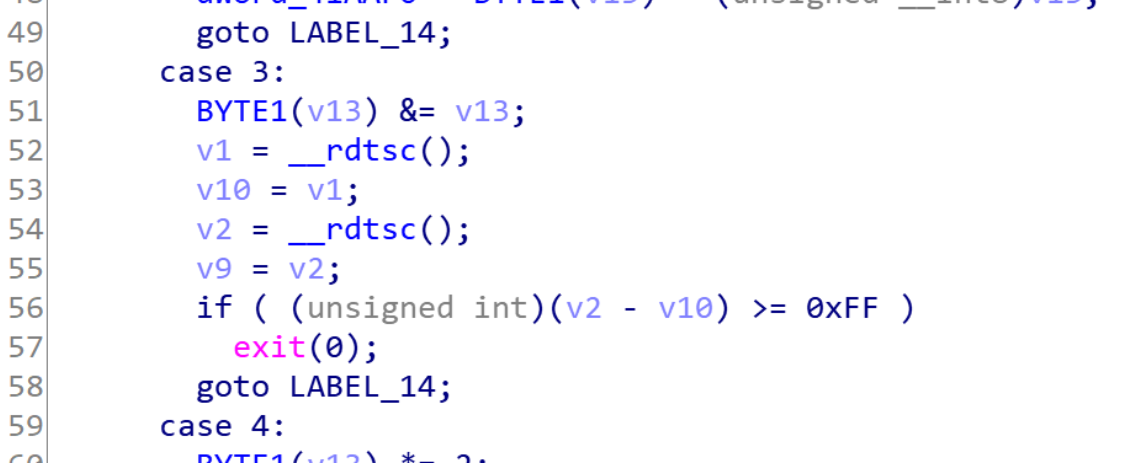
动调得出主要逻辑：flag进行两轮加密，每次取table中的对应位异或和相与，若相与后，结果不为零则将table处值*2继续异或相与。最后将异或的值与后一位flag相异或。

分析逻辑，三位flag是有关联的，猜测flag格式为“flag{}”，动调下断点，发现前几位与对比数据已经相同，并且不受后方未确定字符影响。所以选择爆破flag。python模拟程序加密，按位进行爆破。

python脚本：

cipher=[0x1F, 0x18, 0x0F, 0xFA, 0xB8, 0x63, 0x64, 0x89, 0x18, 0x68, 
 0x7C, 0x19, 0x14, 0x2D, 0x7D, 0x58, 0x00, 0x1E, 0x54, 0x6A, 
 0x41, 0x3C, 0x36, 0x3E, 0x56, 0x13, 0x04, 0x3B, 0x2E, 0x4B, 
 0x79, 0x43, 0x7A, 0x22, 0x45, 0x6E, 0x3A, 0x75, 0x26, 0xC8, 
 0xC0, 0x8E]
table=[9, 2, 7, 8, 6, 9, 11, 10, 4, 11, 12, 4, 7, 7, 10, 4, 3, 9, 4, 6, 3, 12, 11, 13, 
4, 10, 7, 7, 2, 6, 6, 12, 9, 14, 7, 8, 11, 13, 14, 12, 4,7]
table2=[13, 8, 12, 10, 3, 9, 5, 12, 13, 11, 12, 7, 6, 10, 8, 9, 13, 8, 5, 10, 7, 
13, 4, 13, 2, 12, 10, 12, 9, 7, 14, 5, 11, 7, 13, 7, 13, 11, 5, 14, 6, 10]
 \#  print()]
  \# X=(ord('f')^o)&o
  \# if X==0:
   \# print(o)
\#  break;
 \#  else:
   \# o=X*2
def check(flag,P):
  \#flag="flag{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}"
  first=[]
  for i in range(0,41):
​    H=ord(flag[i])
​    \#i=0x7b
​    a=H^table[i] #125
​    b=H&table[i]
​    \# print(b)
​    while(b):
​      k=2*b
​      b=a&k
​      a=a^k
​    \#print(a)
​    first.append(a^ord(flag[(i+1)%42]))
  H=ord(flag[41])
​    \#i=0x7b
  a=H^table[41] #125
  b=H&table[41]
  \# print(b)
  while(b):
​    k=2*b
​    b=a&k
​    a=a^k
​    \#print(a)
  first.append(a^first[0])
  \# for i in first:
  \#  print(hex(i),end=" ")
 \#  print()
  first1=[]
  for i in range(0,41):
​    H=first[i]
​    \#i=0x7b
​    a=H^table2[i] #125
​    b=H&table2[i]
  \# print(b)
​    while(b):
​      k=2*b
​      b=a&k
​      a=a^k
​    \#print(a)
​    first1.append(a^first[(i+1)%42])
  H=first[41]
​    \#i=0x7b
  a=H^table2[41] #125
  b=H&table2[41]
  \# print(b)
  while(b):
​    k=2*b
​    b=a&k
​    a=a^k
​    \#print(a)
  first1.append(a^first1[0])
  \#for i in first1:
​    \#print(hex(i),end=" ")
  \# print()
  \#print(hex(cipher[P]))
  if first1[P]==cipher[P]:
​    return 1
  else:
​    return 0
flag="flag{"
list1="1234567890-abcdefghijklmnopqrstuvwxyz{}ABCDEFGHIJKLMNOPQRSTUVWXYZ"
for i in range(5,41):
  for j in list1:
​    flag1=flag+j+"a"*(42-len(flag)-1)+"}"
​    \#print(flag1)
​    if(check(flag1,i-2)):
​      \#print(flag1)
​      flag+=j
​      print(flag1)
​      break

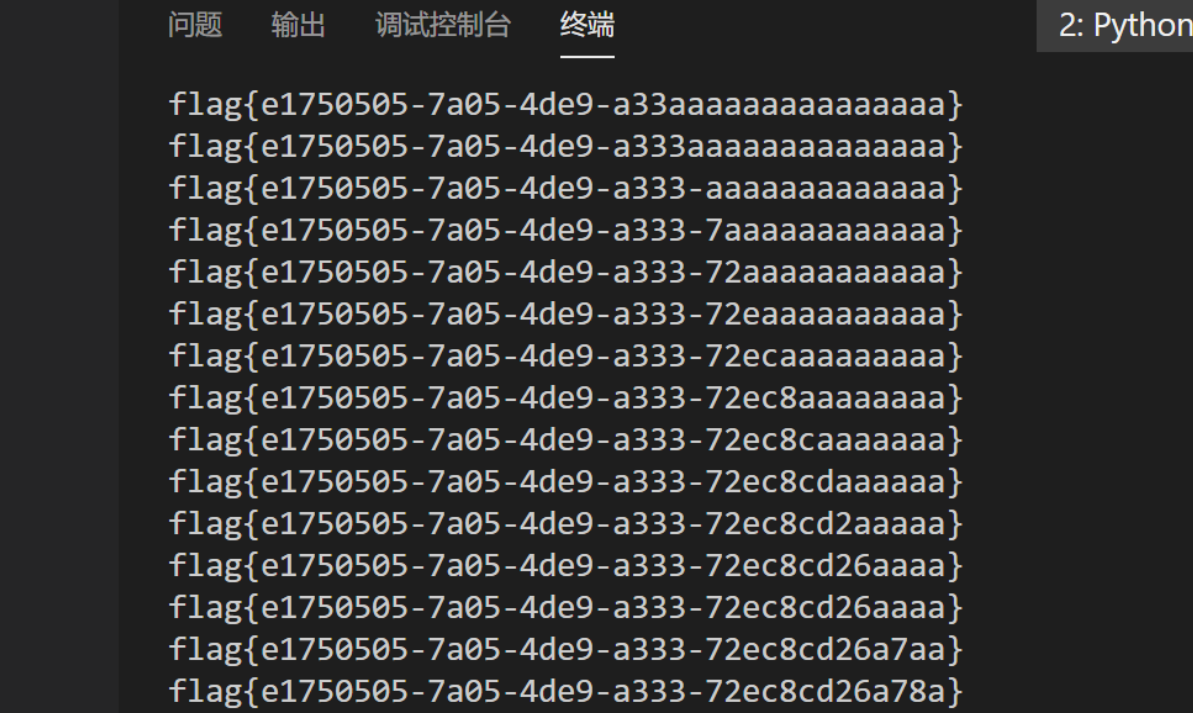
得到flag：

crypto

baby_rsa

思路：根据hint1和hint2求得p从而解题

过程：

hint1 = pow(233*p1+q1,123,n1)
hint2 = pow(p1+q1,321,n1)
t1=pow(hint1,321,n1)
t2=pow(hint2,123,n1)

使hint1与hint2有相同的指数，由于q1前面数字为1，所以可以通过t2-t1来消除掉q1，从而提取出因子p1。

import gmpy2
from gmpy2 import *
from Crypto.Util.number import *
n=17649959524397760997121068808256580843504587497910149453915162267396485718887518595291066193109877306674118444195689568088263844046660375223625289837992862053279345177671592293911174778827999488542179620983366850016034027115530276422989943300228066482304416809472413052663535805445730178026554076921827725694259203653909224978173857255494234555062560049936771927672590813681897238186260507539943545237569643120449213465796499750961465626495972566123774033404378255591053613115928255568749091129063492156842873395480632444228696955053141918113950854532182678159336565263274798149079981609244430557152399984535126235363
c=15029318220576201468560263535467919662488860043345492393144032736965870242713450606659777890850505132225711280093046172524095525322154673926523304203423191705454071359296529857716754655771123283983880428698763018843822679367577019725819696194151686979021896785125371586584321924453460309048191160124062645590495288978330433202359745254888236717638151156562967968775572180730587161672905799413277059329869890946648167796801765219831746094281346814783939724111424859058879220880599487372955861808493657218563898884555812145492576092463968720535434333471337338652526644364433874563267556126777216068855825634384513829424
n1=11941055546120835541933837916957535027223641642056156743752345801163456170772591807989846005495118671627583480778591488285910051133125545781378893719554427584148075540206612251653456701817071613890721071975616517809857996246607186607334395902967699076560894499607006508473605653089963092771854212576322017350805147649094768237953455009748131863337396511143680074932058392590124680763754449521538152648826051051725262170054340100951449328841662181738885435084388023374118710392556656584562494466181529819874959240003672308773193993983011133478065179503497212335076082903214298387572478483167372666139510894330498063363
c1=6581154435167641787433706075004561388301805860331946235823513860405803778235872737931884851831035226083382029584246800645018019413127765759061141252000392053167257633079915212463877266874219355926577661560935087214076228489015179444896502239970526394611817785461522402281447698895527412078173938006497062776091893518267645893781893160963255732937916279470200335626401698825349254177657209090710482565606571789980792435731381726512181109745347022096351073206312644630716411754744858295344041386540535791304586399357404127194796021552916370709209765337503596373097584818783365858724366310222037341353418913289811053095
hint1=1833359454277884547260964954436531463268066576658722989627564649033696969709536217088486700312933027950428272129950495535027288886651991915165684324611000436088979018485688408816231521968453936075696805751053276363477053225197411503384438465457747778257828546056452288773844510523924632927812430649476760238174873630670747649726829664710227729046538241685027106636190022704674813914658555522704254026934170921180880364524978980605216421102751036031187837852845145176233340544629656075196693935478996314670725777034314862269533476603759021249576881724904714872278034418134979560765768103587371983746026587223025082701
hint2=9228372398106611678286602895979417641404959178255543814408337636177265187498562357680073193750915958259886134885485814072189036077766844561767759359250327303362810094050654309593039106720830526510922411657244536811556192653039479590127726241656703727857177346638244353889205681446185783145149422115271311856344478861088252744224041700828934971839656845962952500398770632343211042957147026294673482712989723897728337948158121202913573351729397106490347537538903650384995023749669582138437808423835983027756877883503757939832290271053227076409279478395525689458736619490567940661071408166381129935073856561201013361053
n2=23455941227615775239443656539308297643982180829894484654402049952011754902910673016959293180763361297198028854846363769063194531340669913995607156520854107236145047519578431507504734946246387233119717455988604342629143169157458584024447539175522986194131420361207058659457842367747225416115718224096447064601381167752066587897491480906570491639285673739647530780716845522767589953844752161693528538842719783969776712946980214527220333249829977678665044026275482383388141550463655788551517246509583964301299148891187023831298370935139952329286769019479750190899942260635809156294531533965944585308646875084207341309299
c2=10715530306324673951548363119599726709032302490502503621262820402900708789479621786122202992270558740188089762633055937315273764776127007864314674666166396689989930966418725350921051566929420570800769227599053763394381881199633177787353312804172567883872711505640718496347152167195080365353610444414595776482688285765982794405522837470961426021769204869380013321460287585054427869064253751275281437353126670344963886123242042442941517661063614551338654515719677153884859086613947232523675577273003475854186999077452645748496990780555934158380320022165991608812421649555260206052852131416556798379301864938588470069672
hint3=1654703003093197323980549268127925734263220180218064821197891025480097895203898772683216556991095679066676330439571583420844073504061955914501552694851614664535404506850987626495748207864609522112425305618610542301021476293897450207456755153556758668114136827972390250711416496872911351908708498414711360774971803573424205005228478582765383952861132873141928265470739139939621697690745206102955277335631722299407771944405392356152203059038634579646087719909219308328870723043866071044134819385941485815488954689419436803675260443857367260605145787282706903883937049863141720288267973088830357903178618320711954941279581318770659585316616595448063292922358711609246297827512125769079432138746015092937410075719218112875217464130311880766565746303930574642167673189222237455675759570092101319641817787110871628322729294716699165480945617248862043371295021999756247543649749491705260692788753355626196854460802924198436342429850
#hint1 hint2
t1=pow(hint1,321,n1)
t2=pow(hint2,123,n1)
x1=t1-t2
x2=t2-t1
xx = gmpy2.gcd(x2,n1)
p1 = 111260936618891036068652208614496645952776413871721160526197362367054114767347494528257565447229196035984168278796498545668532710414950556409048002275825950676900234517459096095264009412617416429176073580216701699837149712564123810225413587649986801062654943062839747848949602864178056960224292368694023834399
e1 = 264769
q1 = n1//p1
p1 = mpz(p1)
q1 = mpz(q1)
e1 = mpz(e1)
phi1 = (q1-1) * (p1-1) 
d1 = gmpy2.invert(e1, phi1)
p = pow(c1,d1,n1)
print(p)

q = n//p
#print(isPrime(p))
#print(isPrime(q))
e = 65537
p = mpz(p)
q = mpz(q)
e = mpz(e)
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c,d,n)

print(long_to_bytes(m))

baby_dsa

from Crypto.Util.number import *
from hashlib import sha512,md5

def hash(message):
	return int(sha512(message).hexdigest(), 16)


def sign(message, pubkey, privkey, random1):
	p, q, g, y = pubkey
	x = privkey
	k = pow(y, x, g) * random1 % q
	r = pow(g, k, p) % q
	s = inverse(k, q) * (hash(message) + x * r) % q
	return r, s

public = (3297226463037324458008837284498963372649038889390685051849680175016505646001761220109858921624266044035133134135402561235635833428206886888308027772353030767400921078346868377298401213812053250316002033941692272192644613252296579884516731560436501073253924457646558698855484781747029397755111633297587215976579633451933658235385386539518006570069653575146060016811911140614606471930327341368582979836042585406811352236326065292636484550807213756482153084427714549694264685695977531537425682212155553568848666088576932888234659355213664909753781753917401161977762663658097504411914908081677033980915039079517766159760522261279115347385813009437510156898969769563687869495721977265444799585634019880951532080217960456901788918439265788169910062822889580199366417455186595489973000351770200485095008494228829300145039695936946379585625051402553034971207474762463147744467360158847593356030745194143276254949463650698210515569533, 82302835442112137125891403368151249910268706824854786126600390413622302196443, 1156233264299340971106498371495495695225880592354374034142195518472540521911699506391311324676590685365234887170345722135060009885002334748836477169806166169806180231794918961214520698361874839110454610266388341977984902756569838594616255112661600466818870137432772800368859461445854700956291885576855069405183771903076277144927769029433730710613058788277691211698675287829143272152835171859480781061918556840079857761203012054552142555673071865310355331986288606422711525790877591376770834180618492794265362178603111236615495225612101250344421932588038244804199229449738675082560512062564365473035097263889257937140778993389305893378514344032352806521972367991027459721160744835688761657797398841523104074451793557924512992305640697344011520550723893828185707635141404445213445935586965289450282024222064488965878769991566367115153619761583843561579531705057955933288008556165952066173304891391375100346312776539530448611005, 290999623787731812697719691852061290246619413463636312382146969900546384514710782843153962704851916091601679028830866176332331519515156301401537173069908181509028464322647352256632424684809349121024262597006913707483811117644197481959053785475083406472583099140506505071300193356002443007750220524932219191932969202270343323955035291396808472686684787610559114702054784699365490860392737061056233160308943296478540798353134878937088336672928162894332961762277559345860479916248086821117811990391025187125193074059001086441305977133252774698996653122297123447837449168657347308016270030881395674066421144002959751936839166935726200833785132736328859710351871352567511516142170956091885352178579302299634322254818383978585773136692588922976043617337904545396146755609284163743476297772686548475170197605412847689587171522453229055932712714154869989454808561458852031769119489235598402066924082778376081494632258448434048562053)
p, q, g, y = public[0], public[1], public[2], public[3]

tmp1 = (b'0234e7971889def7e60348f77db94b7a', (10859236269959765735236393779936305217305574331839234502190226708929991582386, 13707557323895695260471053137828523837745895683218331343360027380310980108819))
tmp2 = (b'16c5ac270b72f70319657b4410d985d4', (41960642246379067640524709416001536058292817319109764317369777224426218746518, 74676725322515593502346275468843411563746982149373670021082686341369076719088))
message1, r1, s1 = tmp1[0], tmp1[1][0], tmp1[1][1]
message2, r2, s2 = tmp2[0], tmp2[1][0], tmp2[1][1]
hm1, hm2 = hash(message1), hash(message2)
#print(hm1, hm2)


for random1 in range(1, 512):
    for random2 in range(1, 512):
        random1_inv = inverse(random1, q)
        random_mul = random1_inv * random2
        x = (s1 * hm2 - s2 * hm1 * random_mul) * inverse(s2 * r1 * random_mul - s1 * r2, q)
        x = x % q
        #print(x)
        #print(sign(message1, public, x, random1))
        #print(tmp1[1])
        if sign(message1, public, x, random1) == tmp1[1]:
            print(x)
            flag = 'flag{'+md5(long_to_bytes(x)).hexdigest()+'}'
            print(flag)
            print(random2)
    print(random1)

MISC

签到

{echo,ZmxhZ3t3MzFjMG1lNX0=}|{base64,-d}|{tr,5,6}bash 执行

pcap

frame.len == 91

慢慢找

得到`flag{d989e2b92ea671f5d30efb8956eab1427625c}`

pcap analysis

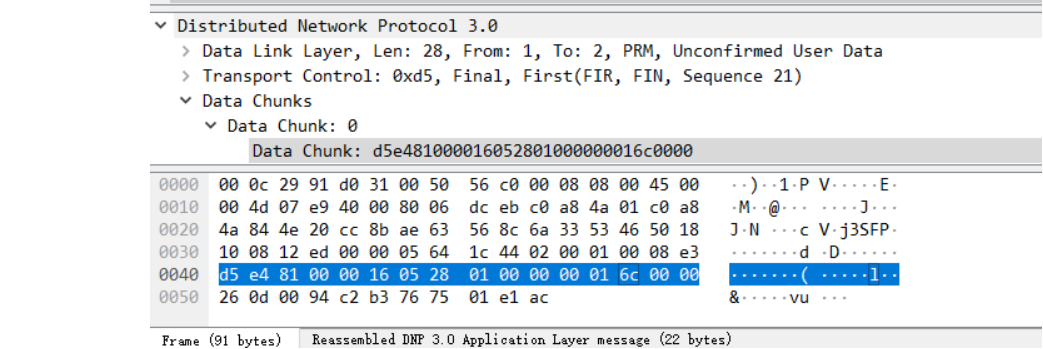
先查modbus,发现有个长度为65,其他都62,与上题基本一样。

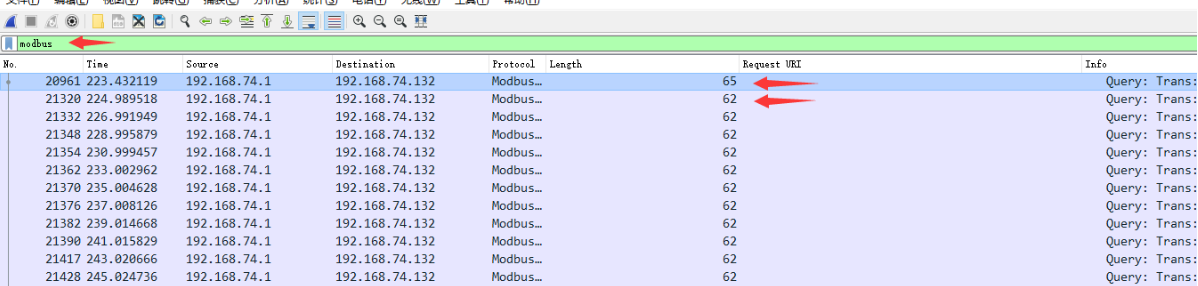
接着直接查frame.len == 65,拼接得到flag

flag{323f986d429a689d3b96ad12dc5cbc701db0af55}